Posts Tagged: r

art / feature / r — 1 Comment
4
Sep 10

Weekend art in R (Part 4)

Computer creations are perfect by design. We put in numbers, and if all goes well we get out an exact result. If we want a line, we want it perfectly straight. If we want a circle, it should conform to the platonic ideal of a circle. From a mathematical standpoint, these perfect shapes and precisely computed numbers are ideal.

Someday, perhaps, we will have true fuzzy computation built right into our hardware. For now, it takes considerable effort to achieve just the right level of imperfection needed for simulating mistakes, or any organic processes.

I sent each of the circles shown above on a random walk. That part was easy, getting each circle to end up where it started (and close the loop) took a bit more effort. To vary the “wigglyness” of the lines, adjust the “sd” parameter in “rnorm”. To change how quickly randomness tapers off, change the “4” in “i/4”. Here is my code:

# Circle lengths
j = seq(0.1,1.9,.08)

par(bg = "black")
plot(-2,-2,pch=".",xlim=c(-2,2),ylim=c(-2,2),col="white")

# How many dots around the circle?
dots = 1000

# Create an offkilter circle
rads = seq(0,2*pi,2*pi/dots)

for(aLength in j) {
	# Pick a random color
	myCol = paste("#",paste(sample(c(1:9,"A","B","C","D","E","F"),6,replace=T),collapse=""),collapse="",sep="")
	
	# Start at length = 1, then walk.
	myLength = rep(aLength,dots)
	
	for(i in 2:dots) {
		myLength[i] = myLength[(i-1)] + rnorm(1,0,sd=.005)
		
		# Closer we are to end, faster we return to where started so circle closes
		dist = aLength - myLength[i]
		myLength[i] = aLength - (dist*((dots-(i/4))/(dots)))
	}
	

	
	for(i in 1:dots) {
		cat(myLength[i]*cos(rads[i]),myLength[i]*sin(rads[i]),"\n")
		points(myLength[i]*cos(rads[i]),myLength[i]*sin(rads[i]),col=myCol,pch=20,cex=2)
	}
}

What do your circles look like?

feature / probability / r — 7 Comments
30
Aug 10

The Chosen One

Toss one hundred different balls into your basket. Shuffle them up and select one with equal probability amongst the balls. That ball you just selected, it’s special. Before you put it back, increase its weight by 1/100th. Then put it back, mix up the balls and pick again. If you do this enough, at some point there will be a consistent winner which begins to stand out.

The graph above shows the results of 1000 iterations with 20 balls (each victory increases the weight of the winner by 5%). The more balls you have, the longer it takes before a clear winner appears. Here’s the graph for 200 balls (0.5% weight boost for each victory).

As you can see, in this simulation it took about 85,000 iterations before a clear winner appeared.

I contend that as the number of iterations grows, the probability of seeing a Chosen One approaches unity, no matter how many balls you use. In other words, for any number of balls, a single one of them will eventually see its relative weight, compared to the others, diverge. Can you prove this is true?

BTW this is a good Monte Carlo simulation of the Matthew Effect (no relation).

Here is the code in R to replicate:

numbItems = 200
items = 1:numbItems
itemWeights = rep(1/numbItems,numbItems) # Start out uniform
iterations = 100000
itemHistory = rep(0,iterations)

for(i in 1:iterations) {
	chosen = sample(items, 1, prob=itemWeights)
	itemWeights[chosen] = itemWeights[chosen] + (itemWeights[chosen] * (1/numbItems))
	itemWeights = itemWeights / sum(itemWeights) # re-Normalze
	itemHistory[i] = chosen
}

plot(itemHistory, 1:iterations, pch=".", col="blue")

After many trials using a fixed large number of balls and iterations, I found that the moment of divergence was amazingly consistent. Do you get the same results?

art / feature / r — 3 Comments
29
May 10

Weekend art in R (part 1?)


As usual click on the image for a full-size version. Code:

par(bg="black")
par(mar=c(0,0,0,0))
plot(c(0,1),c(0,1),col="white",pch=".",xlim=c(0,1),ylim=c(0,1))
iters = 500
for(i in 1:iters) {
	center = runif(2)
	size = rbeta(2,1,50)

	# Let's create random HTML-style colors
	color = sample(c(0:9,"A","B","C","D","E","F"),12,replace=T)
	fill = paste("#", paste(color[1:6],collapse=""),sep="")
	brdr = paste("#", paste(color[7:12],collapse=""),sep="")

	rect(center[1]-size[1], center[2]-size[2], center[1]+size[1], center[2]+size[2], col=fill, border=brdr, density=NA, lwd=1.5)
}
feature / plot / r — 1 Comment
28
May 10

R: More plotting fun with Poission

Coded as follows:

x = seq(.001,50,.001)
par(bg="black")
par(mar=c(0,0,0,0)) 
plot(x,sin(1/x)*rpois(length(x),x),pch=20,col="blue")
feature / games / r — 6 Comments
28
May 10

The guessing game in R (with a twist, of course)

Maybe you remember playing this one as a kid. If you are about my age, you may have even created a version of this game as one of your first computer programs. You guess a number, the computer tells you if you if you are too low or high. I’ve limited the number of maximum guesses, and randomized the computer’s choice based on the Poisson distribution (more on that later).

Here’s the code. This was part of my attempt to understand how R reads input from the command line. One of the things I learned: you may need to save this to a file and run it with “source()”, instead of running it directly from the console, line by line.

# Classic guessing game with twist
x = 0
gotRight = 0
failed = 0

# Initial lambda for our random var
correct = 2000
initial = correct

# How many guesses should we allow per number
maxGuesses = 7
	
while(x != Inf) {
	# The +1 part makes sure we never get zero, which would trigger 0's forever
	correct = rpois(1,correct) + 1
	
	# The advantage of using "cat" instead of "print" is that you remove those pesky quotation marks
	cat("I am thinking of a number between 1 and infinity. What is it? (Type Inf to quit)\n")
	
	# Solicit input from the user
	x = scan(n=1) # Just one item in this vector
	
	# Be nice and let the user quit. 
	if(x == Inf) {
		cat("The correct answer was", correct, "\n")
		cat("You got", gotRight, "right and failed", failed, "times. Maximum allowed guesses was", maxGuesses, "and initial lambda was", initial, ". Goodbye.\n")
		cat("Post your score to http://www.statisticsblog.com/2010/05/the-guessing-game-in-r-with-a-twist-of-course/#comments \n")
		break
	}
	
	for(i in 1:maxGuesses) {
		if(x == correct) {
			print("You rock!")
			gotRight = gotRight + 1
			break
		} else {		
			if(i == maxGuesses) {
				cat("You ran out of guesses. I will pick a new random number based on the last one.\n")
				failed = failed + 1
			} else {
				if(x < correct) {
					cat("You are too low. Guess again.\n")
				} else {
					cat("You are too high. Guess again.\n")
				}
				
				x = scan(n=1)
			}			
		}
	}
}

Note 1: My code makes a couple uses of the aparently controversial "break" function. I can still recall a heated debate I had with a CS professor who believed that calling "break" (in Python) was as bad as crossing the streams of your Proton Pack. That said, I have sucessfully used it on several occasions now without any appearance by Stay Puft Marshmallow Man or changing the natural order between dogs and cats. In R, the biggest problem with using constructs like "break" and "while" is that, for reasons clear only to readers of this blog but not myself, if you ask R for help about either of these tokens using 

?term

you get an sent an error or to purgatory, respectively.

Hint: Because the random guesses are Poisson based, using a "half the distance" strategy for guessing may not be the best way to go. The hardcore amongst yourselves might want to calculate the median of the expected value conditional on having guessed too low or high.

Note 2: The Poisson isn't a very good distribution for for this. Maybe you can find a better one, or at least jack up the dispersion like an overzealous offroader tweaking the suspension of his 4Runner.

feature / r — 1 Comment
26
May 10

Zone of instability

I woke up from my afternoon nap feeling a bit off-kilter, so I decided to go for another random walk. In particular, I wanted a journey that avoided the center, but didn’t just run for an exit either. After playing around for a while I came up with this:

# Take a wacky walk, return the final "track" steps
wackyWalk <- function(iters, track=iters) {
	locations = c()
	mean2use = 0
	sd2use = 1

	for (i in 1:iters) {
		mean2use = rnorm(1,mean2use,sd2use) 

		# The farther from the center, the smaller the variance
		sd2use = abs(1/mean2use)
		if(track > (iters - i) ) {
	 		locations = c(locations, mean2use)
	 	}
	}
	return(locations)
}

# How many steps to take
iters = 300
track = 300
locations = wackyWalk(iters,track)

# Start us off with a plot
plot(0,0,xlim=c(min(locations),max(locations)),ylim=c(0,iters),pch=20,col="white")

for (i in 1:track) {
	points(locations[i],i,pch=20,col="blue")

	# To create a pseudo animation, take a break between plotting points
	Sys.sleep(.10)
}

Basically, during each iteration the program samples from a normal distribution centered at the same location as the previous iteration, with standard deviation equal to the inverse of the previous location. So if the sequence is at 5, the next number will be sampled from the [latex]Normal(5, (\frac{1}5)^2)[/latex] distribution.

Run it a few times and you’ll see how the blue dot bounces around for a bit near 0, then shoots off to one side or the other, where it will most likely hang out for the rest of its life. There are a number of interesting questions about this sequence which, sadly, will remain unanswered. Among these are: For a given number of iterations, how many times is this sequence expected to cross zero? What is the maximum (or minimum) value the sequence is expected to obtain over a fixed number of iterations? Will the sequence ever diverge to some flavor of infinity?

My hunch for this last question is to say no, since the normal distribution is thin-tailed, and the standard deviation is set to converge to 0 (slowly) as the value of the sequence gets larger and larger. At the same time, I suspect that the higher the number of iterations, the larger (in absolute terms) the final number in the sequence. This makes general sense, as the farther you get from 0, the harder it is to return to 0. During testing, I saw a lot of plots that wiggled back and forth, getting closer to the edges of the plot with each wiggle. Since I’m never content to just have a thought without actually testing it out, I plotted the final value in the sequence after [latex]2^x[/latex] iterations, where x went from 1 to 20. Here’s the result:

Sure enough, as a general trend, the more iterations you run, the farther you are from zero. It would have been interesting to see how the 8th trial ended up north of 300, but I only tracked the final result for these. I suspect that it made up most of the ground in a single leap while sampling from a Normal with extremely high variance (ie when the previous number was very close to 0).

Here’s the extra bit of code for comparing final location to number of iterations:

# How does the number of steps compare with distance from center
meta = c()
for (j in 1:20) {
	iters = 2^j
	track = 1
	meta = c(meta, wackyWalk(iters,track))
}

plot(1:20, abs(meta), pch=20, col="blue",xlab="2^x",ylab="abs value of final number in sequence")

These results, I should note, provide very little evidence that the sequence, if extended out to infinite length, will have to converge or diverge. Weird things happen when you start to consider random walks of infinite length, and the one sure limitation of Monte Carlo testing is that no matter how long let a computer simulation run, your PC will crash well before it performs an infinite number of calculations, and most likely before you finish your coffee.

feature / r / stats — 9 Comments
25
May 10

How many tanks? MC testing the GTP

It’s 1943 and you work for the good guys. A handful of German tanks have been captured, and each one has a serial number. This is back when serial numbers were still presumed to come in serial, one right after the other. Given your collection of numbered tanks, and assuming that any existing tank was just as likely to be captured as any other, how many tanks would you guess that the Krauts have?

By luck, you have a time machine, so you jump forward in time, check out the Wikipedia entry, and copy down the formula [latex]\hat{N} = \frac{k+1}{k} m – 1 = m + \frac{m}{k} – 1[/latex], noting that [latex]m[/latex] should be replaced with the highest serial number encountered, while [latex]k[/latex] represents the number of tanks captured. Reading on, you see that Wikipedia has provided a rare nugget of actual understanding for a formula. This estimate represents “the sample maximum plus the average gap between observations in the sample”.

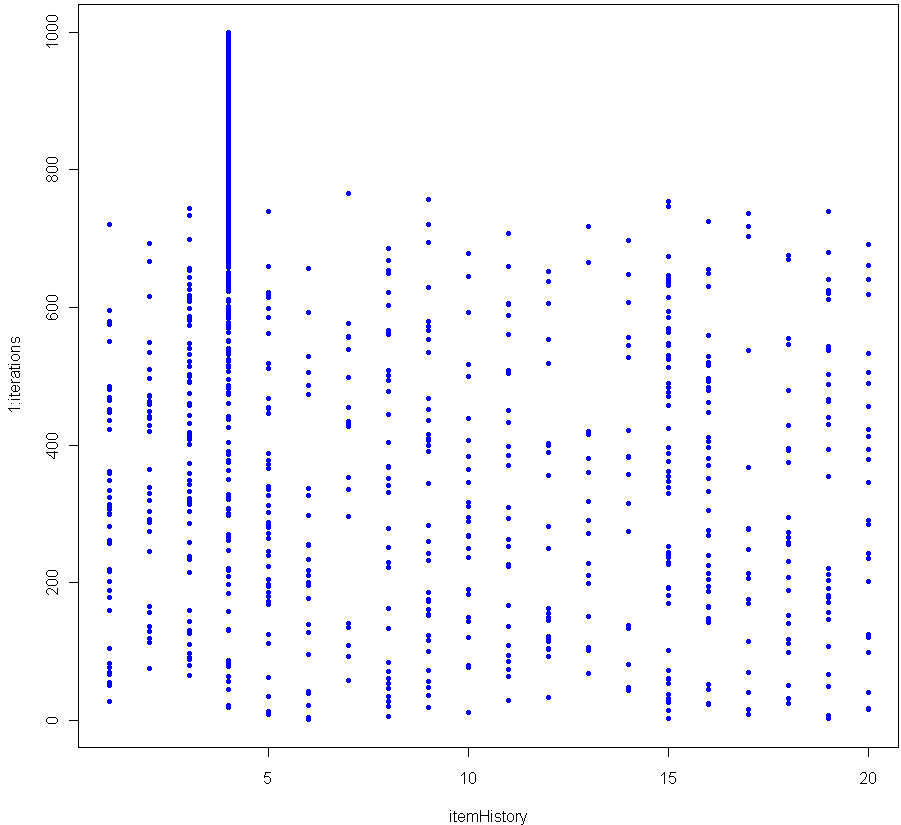
So you’re done, right? Just plug in to the formula, hand in your estimate to the commanding officer, go enjoy some R&R. Not so fast. Here at StatisticsBlog.com, nothing is believed to work until it passes the Monte Carlo test. To test out the formula I coded a simulation in R:

# Function to estimate maximum from sample "samp"
gTank <- function(samp) {
	 max(samp) + max(samp)/length(samp) - 1
}

# A blank log-log plot to get us started
plot(100,100, xlim=c(100,10^7), ylim=c(100,10^7), log="xy",pch=".",col="white",frame.plot=F,xlab="True value",ylab="Predicted")

# Let's track residuals
trueTops = c()
resids = c()
sampleTops = c()

x = runif(100,2,6)
for(i in x) {
	trueTop = 10^i
	for(j in 1:50) {
		observeds = sample(1:trueTop, 20) # No replacement here
		guess = gTank(observeds)

		# Plot the true value vs the predicted one
		points(trueTop,guess,pch=".",col="blue",cex=2) 

		trueTops = c(trueTops, trueTop)
		resids = c(resids, trueTop - guess)
		sampleTops = c(sampleTops, max(observeds))
	}
}

# Platonic line of perfectly placed predictions
lines(c(100,10^6),c(100,10^6),lty = "dashed",col="gray",lwd=1)

# Plot residuals too
windows()
plot(trueTops,log="x",resids,pch=20,col="blue",xlab="True value",ylab="Residual",main="Residuals plot")
abline(h=0)

mean(abs(resids))
mean(trueTops-sampleTops)

Which produces the following log-log plot:

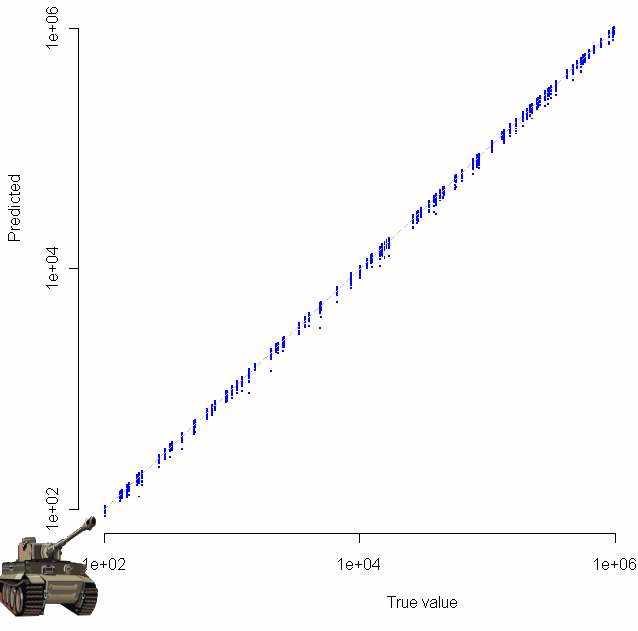
Gratuitous clip art was added with the “chartJunk()” function.

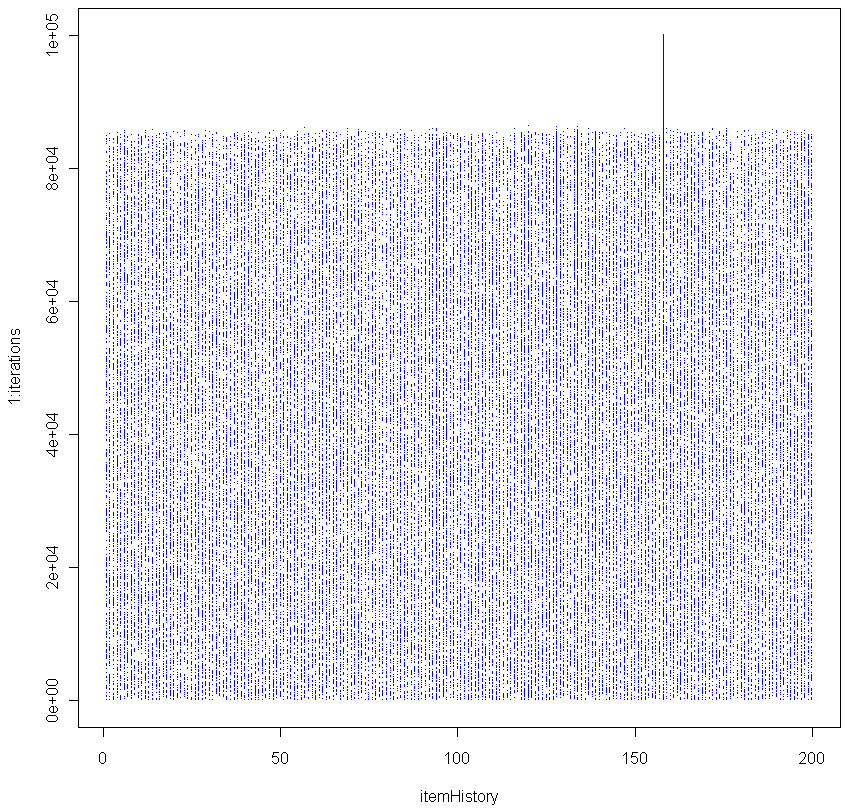
Looks pretty good, no? Especially given that the sample size for each of these tests was just 20. To make sure everything was OK, I plotted the residuals as well:

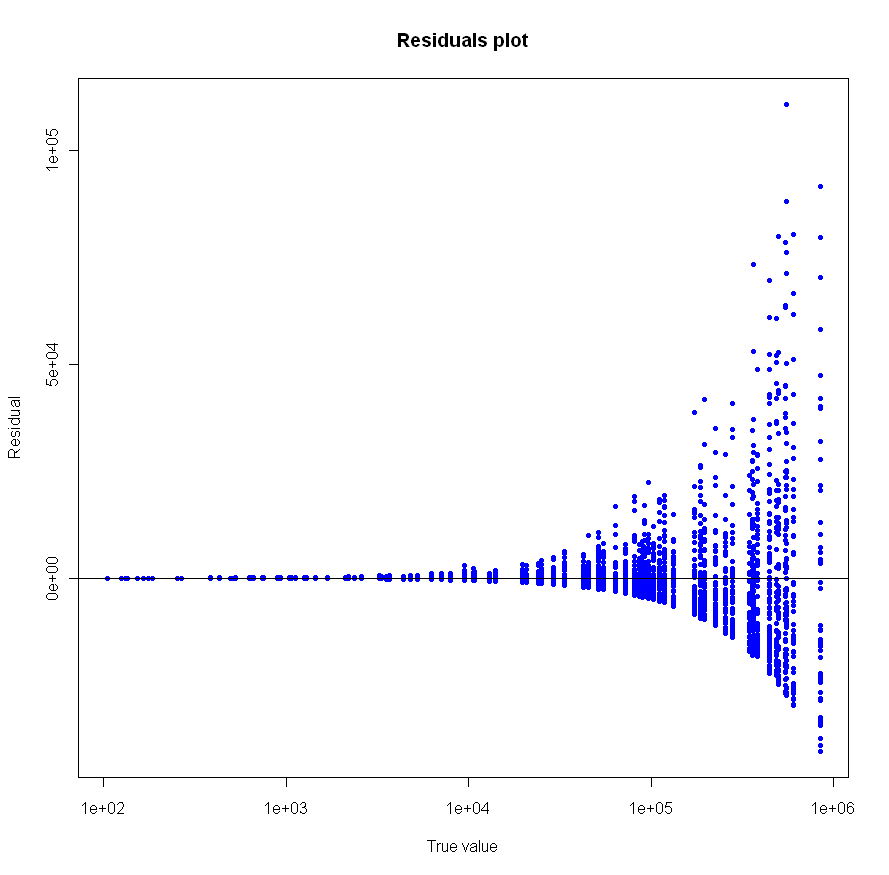
Make sure to click on the images above to see larger versions. Bigger really is better when it comes to viewing charts. Looks good too, no?

So, German tank problem estimate? Confirmed. Just don’t dig too deep into the assumption that all tanks had an equal chance of being captured; common sense goes against that one (ask yourself if there might be a relationship between length of time a tank is in the field of battle and the likelihood it will be captured).

Speaking of likelihood… this problem gives a nice example of how maximum likelihood estimation (MLE) can fail in spectacular form, like a bomb whose innards have been replaced by sawdust (alright, I promise, last military analogy). The MLE for the number of German tanks is the highest serial number observed. This is because MLE works backwards, finding the parameter which makes our observation most likely in terms of joint conditional probability. As a result, the MLE for this problem is not only biased (since it will always be less than or equal to the true number of tanks), but dumb as well. How likely is it (in the common sense usage of the term) that your captured tanks will include the highest-numbered one? If the distribution is truly uniform, the chance that you have to top one is [latex]\frac{k}N[/latex] where [latex]N[/latex] is the true, unknown number of tanks. You don’t know [latex]N[/latex], but you do know that it’s at least [latex]m[/latex] (the highest number observed). For small samples, where [latex]k << m[/latex], the probability that you have captured the very top-numbered tank is quite small indeed, no larger than [latex]\frac{k}m[/latex] at best.

Just how bad is the MLE? I compared the mean absolute residuals from the two different methods. Using the formula from at the beginning of this post gives 6,047. Using MLE, the average residual was 8,175, or 35% worse. Standard deviation for the MLE method is also higher, by about 27%. Back to boot camp for the MLE. (I know, I know, I promised).

feature / r — 2 Comments
20
May 10

R: A random walk though OOP land.

If you are used to object oriented programing in a different language, the way R does things can seem a little strange and backwards. “proto” to the rescue. With this library you can simulate “normal” OOP. I found the examples for proto not so helpful, so to figure out how the package works I sent one lonely red ant on a drunken walk. Here’s my code:

 
library("proto")

# Everybody likes ants
ant <- proto(
	# Default values for the class variables
	xPos = 0,            
	yPos = 0,
	name = character(),      
)

# What do ants do? They move
ant$move <-function(.,xDisp=0, yDisp=0) {
	.$xPos = .$xPos + xDisp
	.$yPos = .$yPos + yDisp
}

# See the little red ant move
ant$plot <- function(.) {
	points(.$xPos, .$yPos, pch=20, col="red")
}

# Instantiate the class. 
myAnt = ant
myAnt$name = "George"


plot(myAnt$xPos, myAnt$yPos, xlim=c(-10,10), ylim=c(-10,10), pch=20, col="red")
for(i in 1:40) {

	# The ant is drunk on Kool Aid
	myAnt$move(rnorm(1),rnorm(1))
	
	# The ant is lazy and will rest for a moment
	Sys.sleep(.5)
	
	# Plot the new location
	ant$plot()
	
}

cat("The ant named", myAnt$name, "is now located at (", myAnt$xPos, myAnt$yPos, ")\n")
feature / r / stats — Comments Off on R: Dueling normals
18
May 10

R: Dueling normals

More playing around with R. To create the graph above, I sampled 100 times from two different normal distributions, then plotted the ratio of times that the first distribution beat the second one on the y-axis. The second distribution always had a mean of 0, the mean of first distribution went from 0 to 4, this is plotted on the x-axis.

Here is my code:

 
AbeatsB <- function(a,b) {
	sum(a>b)/length(a)
}

x = seq(0,4,.001)
y = c()
for (i in x) {
	y = c(y,AbeatsB(rnorm(100,i),rnorm(100,0)))
}

plot(x,y,pch=".",cex=2,col="blue")
← Older Entries
Newer Entries →