epistomology

epistomology / feature / stats — 4 Comments
10
Oct 11

Drop in confidence

I’ve been paying a lot of attention lately to how statistics are released to the public. In particular, when are confidence intervals used, and when are they dropped? When are numbers presented as fact, and when are they acknowledged to be fuzzy?

The only time you consistently see confidence intervals reported, in the general press, is for poll results. As in: 66% of respondents believed this poll to be self-reflexive, with a margin of error of plus or minus 5%.

Weather reports often have percentages involved, but it would be a stretch to call these confidence intervals. For example, when the attractive meteorologist on Channel 7 tells you that there is an 80% chance of rain tomorrow, they are presenting that as a fact. Behind that number is a computer simulation that may or may not be able to estimate a confidence interval around that 80% number.

Government statistics and estimates, no matter how bad or biased, almost never come with confidence intervals attached. Gross Domestic Product of the U.S. in 2010? Estimated at $14.64 trillion. Confidence interval for that estimate? Probably so bad you don’t even want to know. Or maybe you do?

Are there times when you’ve been surprised to see a confidence interval reported or missing?

epistomology / feature / probability — 6 Comments
21
May 11

Problematic quote of the day

“Ellsberg offered several groups of people a chance to bet on drawing either a red ball or a black ball from two different urns, each holding 100 balls. Urn 1 held 50 balls of each color; the breakdown in Urn 2 was unknown. Probability theory would suggest that Urn 2 was split 50-50, for there was no basis for any other distribution.”

From page 280 of Against the Gods: The Remarkable Story of Risk.

epistomology / feature / stats — 4 Comments
8
Feb 11

Power, p-values, publication bias and statistical evidence

I created this video to show as part of a presentation I’ll be giving next week. Your comments welcome, either here or at Youtube.

epistomology / feature / stats — 5 Comments
31
Dec 10

The year of the anti-model

Here’s how it used to work. You have a hypothesis, something you want to test. You go out, collect a mess of data, then start to build a model. The model is your key weapon for understanding the data. Is there a linear relationship? Fit a regression line. Does a particular variable have an impact on the results? Do t-test and find out. The goal is to make your models clear, interpretable, and above all concise. We all know the more parameters you add to a model, the closer you can get it match the data, whatever the data may be, so avoid the temptation to overfit at all costs. Overly complicated models tell you nothing.

Stick to the process above, and you can claim that your results show not just tendencies and correlations, but meaning. The models, properly tested and fit, offer understanding. Through the use of math and inductive logic, we are able to separate the word into signal and noise, “systematic” trends and “random” variation. Once complete, we know what we know (Gremlins are 87% more evil if you feed them after midnight), and we also know what we don’t know (23% of evil behavior in gremlins can’t be explained by violations of the three rules). As an added bonus, we get bounds for how well we know what we know, and how little we know about what we don’t know.

Models can be incredibly powerful tools, but perhaps their least understood property is how well they fool us into believing that fitting a line through points is the same things as understanding an underlying process.

In 2011 I’m going beyond the model. Instead of understanding, I’ll be striving for accuracy of prediction, or to optimize some profit/loss function related to the accuracy of prediction. Instead of trying to part the world into signal and noise — the part that can be understood, and the part that must be dealt with as inevitable “error” — I’m going to design a system that treats signal and noise as all one and the same. Instead of using math and algorithms to extract meaning, I’ll be using these tools to decrease the informational entropy of a stream of data. Data will be treated like a dense, tangled and interconnect forest, an entire ecology of information that cannot be split apart, and can only be “understood” by non-deterministic, evolutionary models which grow in complexity and inscrutability as quickly as their real-world counterparts. In my most well-read (and controversial!) post of 2010, I argued that Occam’s razor was the dumbest argument smart people made. In 2011, I’ll try to demonstrate the power of leaving behind the “simple is better” mentality once and for all.

epistomology / feature / probability / r — 9 Comments
5
Nov 10

Livin’ la Vida Poisson

Yes, I did just mix English, Spanish and French. And no, I am not living the “fishy” life, popular opinion to the contrary. Here’s the story. As someone who spends the majority of his time working online, with no oversight, I notice that I tend to drift a lot. I don’t play solitaire, or farm for virtual carrots, but I do wander over to Reddit more than I should, or poke around in this or that market in virtual assets to see if anything interesting has shown up. To some extent this can be justified. Many, perhaps all, of my profitable ventures have come from keeping my eyes open, poking around, doing my best to understand the digital world. On the other hand, at times I feel like I’ve been drifting aimlessly, that I’m all drift and no focus. My existing projects are gathering dust while I chase after shiny new things.

That’s the feeling, anyway. What does the evidence say? To keep track of what I was really doing, and perhaps nudge me towards more focus, I set a stopwatch to go off every 15 minutes. When it did, I would stop, write down what I was doing at that moment, and continue on. Perhaps you can see how these set intervals might provide an incentive to, shall we say, cheat? Especially right after the stopwatch chimed, I knew that whatever I did for the next few minutes was “free”, untracked. So I decided that I would have to write down everything I did during those 15 minute intervals, which worked sometimes, othertimes not so well.

My current solution? Setup a bell which chimes at random intervals, with an average time between chimes of 15 minutes. To hear what the bell sounds like, Go ahead and try it out, I think you’ll find it makes a nice sound. Leave that page open while you read the rest of this post, see how many times it rings.

At any rate, in order to randomize how long the wait was between chimes, I used a little something called a Poisson process. Actually, what I used was the Binomial approximation to the Poisson built from multiple Bernoulli trials, which results in wait times that are Exponential. Wait! Did you get all that? If so, then skip ahead until things look interesting. Otherwise, here’s more detail about how this works:

In order to determine the length of time between chimes, my computer generates a random number number between 0 and 1. If this random number is less than 1/15, then the next chime is in just one minute. Otherwise, the computer generates another random number and adds one minute to the time between chimes. On average, it will take 15 tries to get a number below 1/15, so the average time between chimes will be 15 minutes. However, to call 15 minutes the average is somewhat misleading. Here are the frequencies of different wait times (source code in R at the end):


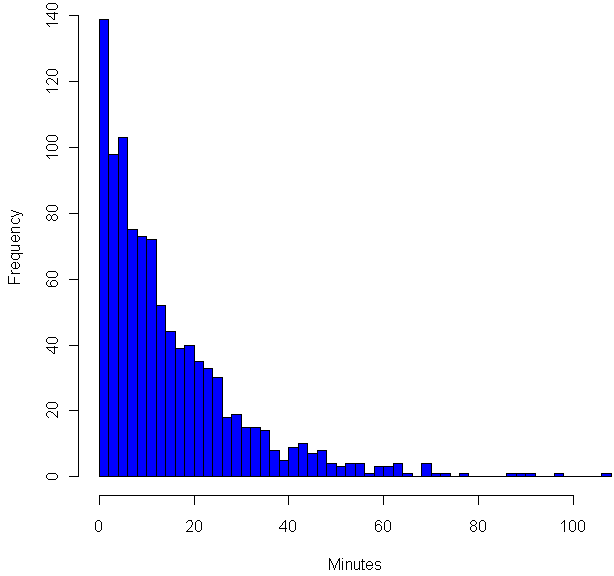
As you can see, the most common time between chimes is just one minute. Strange, no? What’s going on here is that each test to see if the random number is below 1/15 is a Bernoulli trial, which is basically Italian for “maybe it succeeds, maybe it fails”. In this case “success” has probability of 1/15, failure happens the other 14 out of 15 times. In cases where probability is small, and you end of doing a lot of trials, the total number of successes over a given time period will have the Poisson distribution. The “Poisson” here is a Frenchman, who may or may not have smelled like his surname, but who certainly understood The Calculus as well as anyone in the early 1800’s. To get an even better approximation of the Poisson, I could have used trails with probability of success of 1/900, then treated each failure as another second of waiting time. That would have made the graph above smoother.

But wait! I didn’t show you a graph of the Poisson. I showed you a graph of something that approximates the exponential distribution. The number of chimes per hour is (roughly) Poisson distributed, but the waiting time between each chime is exponential, which means shorter wait times are more frequent, but no length of time, no matter how long, can be ruled out. In fact, the exponential distribution is the only (continuous) distribution which is “memoryless”. If you have waited 15 minutes for a chime, your expected wait time is still…. 15 minutes. In fact, your expected wait is independent of how long you have waited so far. The exponential distribution is a “maximal entropy” distribution, entropy in this case is related to how much you know. With the exponential, no matter how long you’ve waited, you still don’t know anything more than when you started waiting.

If you’ve been tuning out and scanning this post, now would be a good time to tune back in. I promise new and interesting things ahead!

It’s one things to understand the memoryless property of the exponential, even down to the mathematical nitty-gritty. It’s quite another to actually live with the exponential. No matter how well I know the formulas, I can’t shake the felling that the longer I have waited in between bell rings, the sooner the next chime must be coming. Certainly, it should be due any time now! While I “know” that any given minute has exactly the same probably as the next to bring with it the bell, the longer I wait, the nearer I feel the the next chime must be. After all, the back of my mind insists, once the page loads the wait time has been set into stone. However it was distributed before, it’s now a constant. Every minute you wait you are getting closer to the next bell, whenever it might have been set to come. I keep wanting to know more than I did a minute ago about about when the next bell will arrive.

This isn’t the only way in which I find my psyche battling with my intellect. I would also swear that over time the distribution of short waits and long waits evens out. Now, by the law of large numbers, it’s true that the more chimes I sit through, the closer the mean wait time will approach 15 minutes. However, even if you’ve just heard three quick bells in a row, that has absolutely no bearing on how long the wait will be between the next three chimes. The expected wait times going forward are completely independent of the wait times in the past. The mean remains 15 minutes, the median remains 10.4 minutes. Yet that’s not what I feel is happening, and over the past two weeks of experimenting with this I would swear that on days when there are a number of unusually quick intervals, these have been followed, later that very the same day, with unusually long intervals. And vice versa. It feels like things are evening out.

It’s possible that when my computer wakes up from a sleep mode, my web browser doesn’t remember where it was in a countdown to refreshing the chime page. So I reload it. Now, in theory, if you “reload” an exponential wait time while in process, this has absolutely no effect on your eventual wait time until the next chime. Yet anytime I reload the page, I have a moment of doubt as to whether I’m “cheating” in some way, to make what would have been a long wait shorter. In this case, the back of my mind says the exact opposite of its previous bias: because I am reloading a page that has been waiting a long time, this means that the wait time would have been really long. By starting the process anew, I’m increasing the chances of a short chime time.

Before you call me a nut, try living for a while with the timer running the background. Keep track of what you are doing if you want (and BTW I’ve found this to be every enlightening and more than a little sad), but mostly keep track of how you feel about the timing. Try reloading the page if you don’t hear a chime for a while. How does that feel? I suspect that in some ways humans were very well hard wired to understand probabilities. Yet I also suspect our wiring hinders how we understand probability, a suspicion backed up by all those gamblers out there waiting for the lucky break that’s well overdue.

CODE:

iters = 1000
results = rep(0,iters)
for (i in 1:iters) {
	minutes = 1
	while(runif(1)>(1/15)){
		minutes = minutes + 1
	}
	
	results[i] = minutes
}

hist(results, breaks=40, col="blue", xlab="Minutes")
epistomology / feature / infinity / probability / Set theory — Comments Off on Seeing angels in the architecture
8
Aug 10

Seeing angels in the architecture

Sorry for the long delay between posts; I was temporarily sucked in to the infinite. While doing some reading about set theory (foundational stuff for probability and, in fact, all of mathematics), I veered off into the infinite and had a hard time climbing back out. I’m guessing you already know most of the basics about sets: compliments and unions and intersections. You may even know some of the stranger parts, like G. Cantor’s cascading crescendo of cardinalities. But knowing those in a cursory way (and really, that’s all a work-a-day statistician or even probabilist needs) isn’t the same as really exploring them.

Looking up again now after several weeks, I feel like I’ve traveled three levels deep in a dream, lost in a purgatory I could only escape by answering questions like  “Is a line made up of points, or does it have points?”, “Is it possible to count what you cannot fully name”, and “In an unbounded universe, is the compliment of the compliment of an object the same as the original object?”. I know, I know. I should have taken that left back at Albuquerque, I shouldn’t have swallowed the red pill. Still, it’s been an interesting trip to say the least, and I feel like I may now be coming back up the the surface, a little bit wiser and a lot more confused than when I began.

Meanwhile, I’ve added a couple items to the “Manifesto” and, The Architect permitting, will be posting a theory on Types of Randomness soon. Post should take between 1 and 10 days to complete, with 95% confidence. Hum… better make that an 80% confidence interval, I still haven’t wrapped my head around the whole idea of forcing.

epistomology / feature — 35 Comments
16
Jun 10

Five dumb arguments smart people make

When smart people make dumb arguments they tend to fall into one of a few categories. I’ve documented five of the most common bad arguments I see at websites where otherwise intelligent geeks, math nerds and skeptics hang out and discuss things. Chances are you’ve encountered at least one of these arguments, maybe you’ve even used one of them yourself.

#1: Occam’s razor

In simple terms, the idea of Occam’s razor is that, whenever possible, simple models are to be preferred. Note that Occam’s razor tells you absolutely nothing about whether a model or a theory is good or bad, useful or worthless. It’s is a rule of thumb. And while not necessarily a bad one, in practice it tends to act like intellect retardant to put out active minds who question existing (often simplistic), beliefs and scientific constructs.

Let me make this very clear: Occam’s razon doesn’t prove anything. In particular, and despite how it is commonly used, it doesn’t show that the more likely, or “simple”, explanation is the correct one. Unlikely, complicated things happen all the time. If you don’t believe this, go flip a coin a thousand times. I guarantee you that the exact result you get will only happen once in a godzillion tries. In terms of (absolute) likelihood, explaining what you just observed with probability theory and stochastic processes is way more complicated than the assertion “that’s what God wanted”, a theory which, if true, explains your effectively impossible result with 100% likelihood. I’m guessing that’s not the can of worms you hoped to open up with Occam’s razor?

#2: You’re a hypocrite.

Yes, and so are you. So what? Do I really need to explain why this agumentum-ad-hypocrisum (note, made-up Latin) is so bad? Given that accusations of hypocrisy are almost as popular as kittens in the blogosphere, I suspect I do. So here goes: showing that your opponent is a hypocrite proves nothing except that they are human. It doesn’t make their arguments wrong, and only weakens them under very limited circumstances, like when you catch a sworn bretharian sneaking a pint of Häagen Dazs to keep from starving to death. Beyond that, calling your opponent a hypocrite has less nutritional value than a peep.

#3: That’s just an anecdote. It doesn’t prove anything.


Repeat after me: Anecdotes are evidence. Nothing more, but certainly nothing less. In the context of a common event followed by another common event (I got a headache after stopping at three red lights in a row), anecdotal evidence is nearly useless. In terms of more rare events (I got kuru after eating my sister), anecdotal evidence can be extraordinarily powerful. Taken to its extreme, discounting anecdotal evidence led (presumably intelligent) academics to hold firm to fallacies like the idea that fireflies can’t flash all in unison, long after anecdotal evidence had come in from reliable observers.

#4: No known mechanism


There are lots of intelligent ways to argue that homeopathy doesn’t work. You can cite studies (although you may find that not all of them confirm your beliefs), or you can say that believers are the random subset of the people who have tried it and then afterwords felt an improvement. I’m not going to weigh in on the subject, except to note that one argument I see used fairly often is that homeopathy doesn’t work because it can’t work, and it can’t work because we don’t understand how it possibly could.

To see how bad this argument is you need to look at the assumptions behind it and view it in historical context. What people are really saying with this argument is: Our current scientific model is comprehensive and infallible. It accounts for all observations, and it has no holes or leaks. I’m going to assume that you are able to see the problem with this mindset yourself. I’ll just note that one particularly unfortunate use of this argument led doctors to reject hand washing before performing operations or delivering babies. After all, evidence that fastidious midwives had lower infection rates was purely anecdotal (see above), and there was no reason to believe cleanliness could make a difference in the pre-germ era. There was no known mechanism.

#5: Three guys with boards


I’m calling this the “three guys with boards” argument in honor of those skeptics who, whenever someone mentions crop circles, declare “it’s a hoax. Three guys with boards admitted they did it.” In fact, some guys with boards did indeed admit to creating a crop circle, and they showed us how they did it. So what’s wrong with this argument?

The problems is that you can’t discount all anomalous observations as “fakes” just because some are known to be fakes, nor does the possibility of faking an event mean that all such events must have been faked. Obviously, scientists don’t like playing games of intellectual wack-a-mole. If you research enough supposed “unexplained mysteries”, and come away convinced each time that the mystery is bogus, the tendency to dismiss other, similar claims outright is understandable. That said, “three guys with boards” is still a dumb argument, especially when you are going against claims of specific evidence that can’t be easily explained away as a hoax. For example, we have large, complicated, precisely implemented crop circles done in a short span of time and exhibiting strangely bent stalks. This evidence may fall far short of irrefutable proof of alien intervention, but it does require much more than dismissively stating that we know they are all fakes. We don’t.

More broadly, any attempt to automatically sort new observations into known categories (often categories that make us comfortable) is a bad idea. Unfortunately there are no shortcuts when it comes to evaluating data or evidence. It has to be done the hard way, one piece at a time.

epistomology / feature / probability — 1 Comment
2
May 10

Anthropic principle visited (because I can visit it)

The Anthropic Principle justifies the existence of life against apparently infinitesimal small scientific odds of a life-sustaining universe. The arguments behind it can be fairly complex, but I think the most important part can be summed up very easily:

“If the outcome had been negative, we wouldn’t be around to witness it.”

In other words, if the universe had been inhospitable to human life, no one would be around to verify what came to pass. Although it is usually limited to justifying life on earth, the anthropic principle goes well beyond the cosmological. It effects how we understand any rare event which happens to happen to us.

Start with an extreme event. A fully loaded bus slides over the guardrail on a mountain pass. Ninety nine passengers die. One survives. It would hardly be surprising if that one passenger says God, and not random luck, saved her. After all, she alone survived, miraculously, while everyone else perished in a wreck which seemed destined to kill everyone.

But how do the other 99 passengers feel? Did God choose them to die, just like He apparently choose her to live? Maybe we could interview them. Oh, wait.

Take thousands of individual events, each one extraordinarily improbable, and try them out with billions of people over and over. The most likely result, the most scientifically probable, is that some people will experience extremely unlikely occurrences. If they go on to ascribe those experiences to more than just blind luck that shouldn’t surprise us. It’s only natural. But it most certainly doesn’t prove divine intervention.

Think of it this way: You, the consciousness reading these very words, are the product of millions of little events which could have just as easily gone the other way: If you mother didn’t have a soft spot for men with mustaches, if you great-grandfather hadn’t been shot down over France, if you great-great grandfather hadn’t bumped his head on that giant bottle of Sam’s Cure-all Tonic, you won’t be here today. You’re as unlikely as a tossed coin landing on its side. The universal probability bound is broken every day.

Of course the same thing goes for everyone else around you. Ten billion souls, each one coming into existence despite near impossible odds. Ten billion miracles, right? Only if you discount the stega-godzillion souls who’s coin flips landed the usual way and were never born. They are mute, silent, YouTube-impaired, invisible non-witnesses to their own bell-curve filling banality.

Newer Entries →