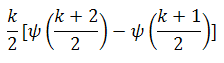There are a few ways to do this, but the only one that worked for me was to use Rserve and rconnect. In R, do this:
install.packages("Rserve")
library(Rserve)
Rserve(debug = FALSE, port=6311, args=NULL)
Then you can connect in Python very easily. Here is a test in Python:
rcmd = pyRserve.rconnect(host='localhost', port=6311)
print(rcmd('rnorm(100)'))
Needed this one recently, it pops up a window to pick a file to be used by r, then reads the contents into myData:
myFile <- file.choose()
myData <- read.table(myFile,header=TRUE)
Before I decided to learn R in a serious way, I thought about learning Flash/Actionscript instead. Most of my work involves evolutionary models that take place over time. I need visual representations of change. It’s certainly possible to represent change and tell an evolving story with a single plot (see for example Tufte’s favorite infographic), but there are a lot more options when you can use animations. Flash is also object oriented, well documented with hundreds of books and websites, and has a powerful (albeit challenging to learn) IDE which helps for large coding projects.
The drawbacks to Flash are that it is way behind R in terms of statistical tools, is a closed, expensive language to work with, and dispute widespread use it might be so weak that a Apple’s iPhone might kill it.
So I picked R, with the idea that when I needed animations, I would find a way to build them. The code below is my first test of using R to generate animations. It’s a variant of Conway’s Game of Life (not to be confused with the Milton Bradley version), where single celled lifeforms live or die based on how many living neighbors they have. In my version, the rules for each cell are determined randomly, in advance of the game. The board size is fixed (see the configuration options at the beginning), whereas Conway’s version was played on a theoretically infinite grid. Green cells are “alive”, black ones are “dead”. I tried for nearly an hour to match the Black=living, White=dead scheme of Conway but couldn’t get that to work, maybe you can figure out how to do it. I re-sized the resulting animated GIF with an external program, that’s another thing I still need to figure out in R.
par(mar=c(0,0,0,0))
library(abind)
library(gdata)
library(fields)
library(grDevices)
library(caTools)
#
times = 50
myWidth = 10
myHeight = 10
#
# Set the 3D array of rules to determine transitions for each cell.
rulesArray = NULL
for(i in 1:9) {
toBind <- matrix(sample(c(0,1),replace=T,(myWidth*myHeight)),ncol=myWidth)
rulesArray <- abind(rulesArray, toBind, along=3)
}
#
first = T
frames = array(0, c(myWidth, myHeight, times))
for(i in 1:times) {
if(first) {
forFrame <- sample(c(0,1),replace=T,(myWidth*myHeight))
first = F
} else {
# Convert last frame data to matrix to make comparing adjacent cells easier
forFrame <- matrix(forFrame, ncol=myWidth)
newFrame <- forFrame
#
for(m in 1:myHeight) {
for(n in 1:myWidth) {
adjLiving = 1 # cuz we start with array index 1
#
# Find out how many adjacent are living
if(m > 1 && n > 1) {
# Look at top left
adjLiving = adjLiving + forFrame[(m-1),(n-1)]
}
if(m > 1) {
# Look at top center
adjLiving = adjLiving + forFrame[(m-1),(n)]
}
if(m > 1 && n < myWidth) {
# Look at top right
adjLiving = adjLiving + forFrame[(m-1),(n+1)]
}
if(n > 1) {
# Look at left
adjLiving = adjLiving + forFrame[(m),(n-1)]
}
if(n < myWidth) {
# Look at right
adjLiving = adjLiving + forFrame[(m),(n+1)]
}
if(m < myHeight && n > 1) {
# Look at bottom left
adjLiving = adjLiving + forFrame[(m+1),(n-1)]
}
if(m < myHeight) {
# Look at bottom center
adjLiving = adjLiving + forFrame[(m+1),(n)]
}
if(m < myHeight && n < myWidth) {
# Look at bottom right
adjLiving = adjLiving + forFrame[(m+1),(n+1)]
}
#
# Find the corresponding rule for this cell
newStatus = rulesArray[m,n,adjLiving]
#
# Update the status of this cell depending on the rule and number of living adjacent
newFrame[m,n] = newStatus
}
}
#
# Pull it out of a matrix
forFrame = unmatrix(newFrame)
}
frames[,,i] <- forFrame
}
write.gif(frames, "gameOfLifeRevisited.gif", col=c("#FFFF00", "#000000") , delay=150)
To start sending all output to a file, do this:
sink("path/to/filename") # Direct all output to file
print("Hi there") # Will be printed to file
sink() # Turn off buffing to file
Related to this I recently had to use:
flush.console()
This forces your console to print out any buffered content. Doing this will cost time, but if you are running a very long script and wonder if it is still alive, you might do something like this:
for(i in 10000:20000) {
# Find the i'th prime number
# Are we still alive?
cat("."); flush.console()
}
$100 to the first person who can figure out how I created this plot and replicate it. Some hints:
rdist()“).This is based on a random sampling of unstated size, so I don’t expect that your graph will be an absolute, exact match.
I’ll add $1 to the prize for every day that goes by without a winner until the end of the year. After that I’ll consider it an unsolved mystery and reveal the code I used.
Post your guesses for the code as a comment to this post. First correct answer wins. Good luck to all!
I found this interesting question over here at mathoverflow.net. Here’s the question:
If you have a country where every family will continue to have children until they get a boy, then they will stop. What is the proportion of boys to girls in the country.
First off, there are some assumptions you need to make that aren’t stated in the problem. The most important one is that boys are just as likely as girls to be born. This is empirically false, but there’s nothing wrong with assuming it for the problem, so long as the assumption is acknowledged.
My first thought about solving the problem was to think about Martingales and stopping times, but that’s more complication than you need. If you look at it from the point of view of expectation things are simpler.The probability of having a boy first is 1/2, at which point the family stops and you have a ratio of 1 boy per 1 births. The probability of having one girl, then one boy is 1/4, at which point you have a ratio of 1 boy per 2 births. Multiplying the probabilities by the ratios and summing from 1 birth to infinity, you get an expectation of approximately 69.31% boys.
Problem is, this is the expectation for a single family. Because families who have more children (and thus more girls) contribute disproportionately to the pool of children, one family is a biased estimator for the proportion in the entire population. Douglas Zare at the above-linked mathoverflow question does a good job of working out the details for a country with an arbitrary number of families. Here is what he comes up with for the percentage of girls:
Where k is the number of families in the country, and 
is the digamma function.
To be true to the new motto of this site, I decided to test this out in R using a Monte Carlo method. Here is my code:
And here is the resulting graph:
Looks like a good match.
Maybe you noticed that at the beginning I mentioned assumptions, as in more than one. We are also assuming that that all of the boys and girls, no matter how old, are still considered boys and girls. All of the parents were already in the country at the beginning of the problem, and then they all started having children until they had a boy and stopped. None of these children have had any children. The process is complete, and the new generation is the last. Obviously even if parents in a country did follow the rule of "babies until boy then stop", the results wouldn't match the theoretical because at any given moment there are many families in the process of still having kids. This is where, if I were so inclined or needed a more accurate model, I would dive back into the Martingale issue and things would get messy.