In their book “Complex Adaptive Systems”, authors Miller and Page create a theoretic model for bee attacks, based on the real, flying, honey-making, photogenic stingers. Suppose the hive is threatened by some external creature. Some initial group of guard bees sense the danger and fly off to attack. As they go, they lay down a scent. Other bees join in the attack if their scent sensitivity threshold (SST) is reached. When they join the attack, they send out their own warning scent, perhaps triggering an even bigger attack. The authors make the point that if the colony of bees were homogeneous, and every single one had the same attack threshold, then if that threshold was above the initial attack number, then no one else would join in. If it were below, then everyone goes all at once. Fortunately for the bees, they are a motley lot, which is to say a lot more diverse than you would imagine just from looking at the things. As a result, they exhibit much more complicated behavior. The authors describe a model with 100 bees and call their attack threshold “R”. By assuming a heterogeneous population of 100 with thresholds all equal spaced, they note:
“In the hetrogeneous case, a full-scall attack ensues for [latex]R \geq 1[/latex]. This latter result is easy to see, because once at least one bee attacks, then the bee with threshold equal to one will join the fray, and this will trigger the bee with the next highest threshold to join in, and so on…. It is relatively difficult to get the homogeneous hive to react, while the hetrogeneous one is on a hair trigger. Without explicity incorporating the diversity of thresholds, it is difficult to make any kind of accurate prediction of how a given hive will behave.”
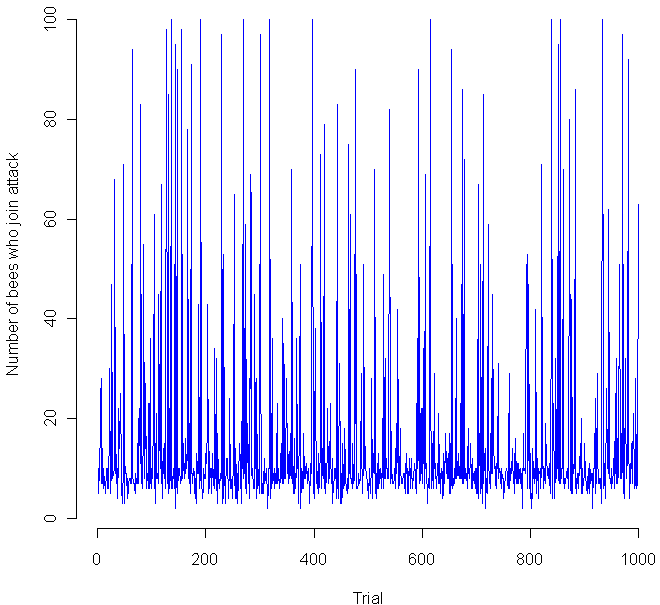
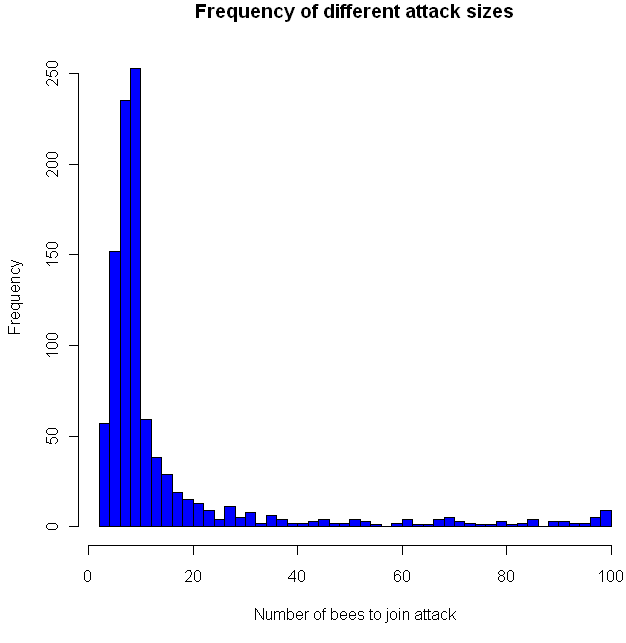
I think this last sentence is their way of noting that the exact distribution of sensitivities makes a huge difference in how the bees behave, which indeed it does. I decided to put the bees to the test, so I coded a simulation in the language R (code at the end of this post). I gave 100 virtual apis mellifera a random sensitivity level, chosen from a Uniform(1,100) distribution, then assumed 10 guards decided to attack. How would the others respond? Would a hair-trigger chain reaction occur? The chart at the top shows the results from 1000 trials. Looks pretty chaotic, so here’s a histogram of the results:
As you can see, most of the time the chain reaction dies out quickly, with no more than 20 new bees joining in the attack. However, occasionally the bees do go nuts, sending the full on attack. This happened about 1 percent of the time. Perhaps most interestingly, all of the other attack levels were clearly possible as well, in the flat zone from about 30 to 95. You might want to try playing with the distribution of the sensitivities and see if you get any other interesting distributions. Meanwhile, if you decide to raid a hive, make sure to dip yourself in mud first, that way the bees will think you are nothing but an innocent black rain cloud.
Code in R:
trials = 1000
go = rep(0,trials)
initial = 10
for(i in 1:trials) {
bees = sort(runif(100,1,100))
# Everyone who's threshold is less than the inital amount goes.
going = length(bees[bees initial) {
more = length(bees[bees going) {
# Keep doing this until it stops
going = more
more = length(bees[bees