Last night, while playing Boggle, we ended up with a board without a single vowel. Not even a “Y” or “Qu”. This seemed fairly unusual, so I wondered what the chances were of such an occurrence. I found an online list of the letters each die has, and I could have written down the number of vowels on each one by hand, but whenever possible I like to do things by computer. So I fired up Hal and asked for some help with the calculations.
Apparently some European boards use a 5 x 5 grid, but here in the land of the Maple leaf our board has 16 cubes. Here are the letters on them, as I coded them into R:
d1 = c('S','R','E','L','A','C')
d2 = c('D','P','A','C','E','M')
d3 = c('Qu','B','A','O','J','M')
d4 = c('D','U','T','O','K','N')
d5 = c('O','M','H ','R','S','A')
d6 = c('E','I','F','E','H','Y')
d7 = c('B','R','I','F','O','X')
d8 = c('R','L','U','W','I','G')
d9 = c('N','S','O','W','E','D')
d10 = c('Y ','L','I','B','A','T')
d11 = c('T','N','I','G','E','V')
d12 = c('T','A','C','I','T','O')
d13 = c('P','S','U','T','E','L')
d14 = c('E','P','I','S','H ','N')
d15 = c('Y','K','U','L','E','G')
d16 = c('N','Z','E','V','A','D')
So now I had to check how many vowels were on each die. Here’s the code I used for this:
vowels = c('A','E','I','O','U','Qu','y')
vowelsFound = rep(0,16)
for(i in 1:16) {
found = 0
die = eval(parse(text=paste("d",i,collapse="",sep="")))
for(l in die) {
# Check to see if this letter is in the vowels vector
if(l %in% vowels) {
found = found + 1
}
}
vowelsFound[i] = found
}
# Probabilities of getting a vowel for each die
pVowels = vowelsFound/6
# Probability of getting no vowel for each die
pNoVowels = 1 - pVowels
# Chance that we will get not a single vowel, including "y" and "Qu"
print(prod(pNoVowels))
If you run the code above, you should see that the probability of getting no vowels (including “Y” and “Qu”) is 0.000642. That works out to one in every 1557 boards. So it’s quite rare, but by no means so extraordinary that it crosses the Universal probability bound. Also, it’s not enough to just calculate how rare your event is, or how rare any similar or more extreme event is, and then be astounded. You also have to include all the other possible events that would have left you amazed. What about getting all vowels (much more rare)? What about getting 8 or 9 E’s, or a row or column of all A’s or E’s? It’s likely that if you add up all probabilities of all the rare events which might leave you amazed, you’ll end up with a good chance of amazement every time.
I could have stopped here, but having coded the dice, I decided to create a simplified version of the game in R. If I have a chance over the next few days I’ll add some more features.
# You will need to download a dictionary file. I found one here:
# http://svn.pietdepsi.com/repos/projects/zyzzyva/trunk/data/words/north-american/owl2-lwl.txt
words = read.table("wordlistData.dat", colClasses = "character")
words = unlist(words[,1])
# Create a random board. Plot it.
board = diag(4)
dice = sample(1:16,16)
cntr = 4
for(i in dice) {
die = eval(parse(text=paste("d",i,collapse="",sep="")))
board[floor(cntr/4), (cntr %% 4) + 1] = sample(die,1)
cntr = cntr + 1
}
plot(0,0,xlim=c(0,4),ylim=c(0,4),col="white",ann=FALSE, xaxt="n", yaxt="n" )
for(m in 1:4) {
for(n in 1:4) {
text(m-.5,n-.5,labels=board[m,n],cex=2.75,col="#000099")
# Draw a square the easy way
points(m-.5,n-.5,pch=0,cex=10,lwd=1.5,col="gray")
}
}
# How many seconds to give for each round
gameTime = 180
START_TIME = proc.time()[3]
elapsed = 0
# Simple scoring, with 1 point per letter.
# Dictionary only has words length 3 or longer
score = 0
cat("Find words. Hit enter after each word.\n")
while(elapsed < gameTime) {
myWord = scan(n=1, what=character()) # Get a single word
elapsed = signif(proc.time()[3] - START_TIME, digits=4)
if (length(myWord)==0) {
cat("You have", gameTime - elapsed, "seconds left. Keep going!\n")
} else {
if(elapsed < gameTime) {
# Check if it's a real word, see if it is in dictionary
# Convert their guess to uppercase letter
myWord = toupper(myWord)
# If it is in the dictionary, give them points
if(myWord %in% words) {
# Make sure they haven't used this word before TODO
# Add it to their score
score = score + nchar(myWord)
cat("Congratulations. You are up to", score, "points.")
cat("You have", gameTime - elapsed, "seconds left. Keep going!\n")
} else {
# If it isn't in the dictionary, let the user know that they got it wrong.
cat("Sorry, that is not in the dictionary. Keep trying!\n")
}
}
}
}
cat("Out of time! ")
cat("Your final score was:", score, "points.")
Enjoy the game. Let me know if you notice any issues or have suggestions!
Tags: boggle

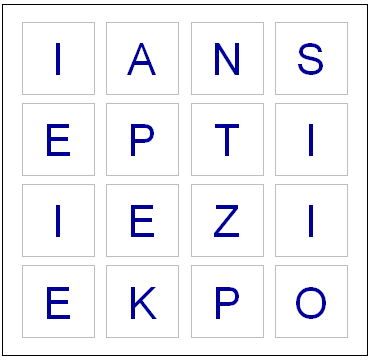
Nice! Lots of fun we play boggle all the time. How about checking for duplicate words and to make sure you can make the word with the board you have.
Are we the same person? I am a graduate student studying biostatistics and the domestic students in our department love playing boggle online! I got addicted to it a few months ago. The one I play is on wordsplay.net. Is it the same one? If it’s the same one, you can join Team Stats!
My husband wrote a LabView program a few years ago which calculated the best possible Boggle score for a given board (given no opponents) based on an exhaustive list of all available dictionary words. A cool bit of programming, but makes Boggle less fun!
Has anyone figured out the probability of observing words of a given length in Boggle? e. g., what’s the probability of a 10-letter word?
Well, since you built it already, could you dust it off and tell me what the probability of getting the word ‘creamers’ is? I will, in turn, buy you a beer next we meet!
Your probability is a little low. Without really looking at your code but doing some math:
Let P(i) be the probability that you get a vowel for cube i. So,
P(i)=1/3 for i={1,2,4,5,7,8,9,11,13,14,16}
P(i)=1/2 for i={3,10,12,15}
P(i)=2/3 for i={6}
Let K= the product of (1-P(i)) for i from 1 to 16; which equals (2/3)^11*(1/2)^4*(1/3)^1 [this is the probability of getting no vowels]
For each i let Q(i) = P(i)*K/(1-P(i)) [this is the probability that cube i is the only vowel]
Each Q(i) is mutually exclusive from each other so the total probability of the event of getting only one vowel is the sum of Q(i) from i=1 to 16.
This simplifies to:
16*K*[11*(1/2)+4*(1)+2*(1)]=11.5K=23*2^6/3^12
This is closer to 1 out of 361. I verified this result with quick spreadsheet.
Now, looking at your code I see a lowercase y in your vowels and uppercase Y in your die. If it is case sensitive I can see the probability being lower than it should be.