Lately I’ve been thinking about how to measure the fatness of the tails of a distribution. After some searching, I came across the Pareto Tail Index method. This seems to be used mostly in economics. It works by finding the decay rate of the tail. It’s complicated, both in formula and in it’s R implementation (I couldn’t get “awstindex” to run, which supposedly can be used to calculate it). The Index also has the disadvantage of being a “curve fitting” approach, where you start by assuming a particular distribution, then see which parameter gives the best fit. If this doesn’t seem morally abhorrent to you, perhaps you have a future as a high-paid econometrician.
In the past I’ve looked at how to visualize the impact of the tails on expectation, but what I really wanted was a single number to measure fatness. Poking around the interwebs, I found a more promising approach. The Mean Absolute Deviation (or MAD, not to be confused with the Median Absolute Distribution, or MAD) measures the average absolute distance between a random variable and it’s mean. Unlike the Standard Deviation (SD), the MAD contains no squared terms, which makes it less volatile to outliers.
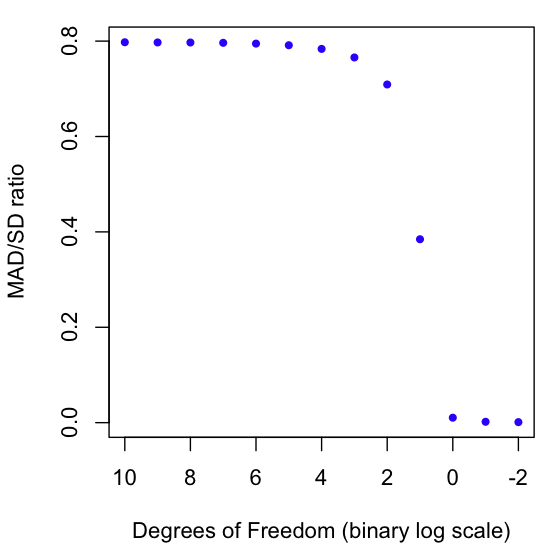
As a result, we can use the MAD/SD ratio as a gauge of fat-tailedness. The closer the number is to zero, the fatter the tails. The closer the number is to 1 (it can never exceed 1!), the thinner the tails. For example, the normal distribution has a MAD/SD ratio of 0.7970, which happens to be the square root of 2 over pi (not a coincidence, try proving this if you rock at solving integrals).
The graph at the beginning of this post shows a Monte Carlo estimation of the MAD/SD ratio for the Student T distribution as it goes from very high Degrees of Freedom (1024) to very low (1/4). You may know that the T distro converges to the Normal at high degrees of freedom (hence the result of nearly .8 for high DF), but did you know that the T distro on 1 Degree of Freedom is the same as the infamously fat-tailed Cauchy? And why stop at 1? We can keep going into fractional DFs. I’ve plotted the ratio all the way down to 1/4. As always, code in R is at the end of the post.
One more thing: there is at least one continuous distribution for which the MAD/SD ratio reaches it’s maximum possible value of one. First person to guess this maximally thin-tailed distribution gets a free copy of the comic I worked on.
# Start with a Normal, move to a Cauchy
dfs = 2^(10:-2)
results = c()
for(i in dfs) {
x = rt(1000000,i)
results = c(results, mean(mean(abs(x))/sd(x)))
}
# Note the wonky x-axis limit and order
plot(rev(-2:10), results, col="blue", pch=20, xlim=rev(range(-2:10)), xlab="Degrees of Freedom (binary log scale)", ylab="MAD/SD ratio")