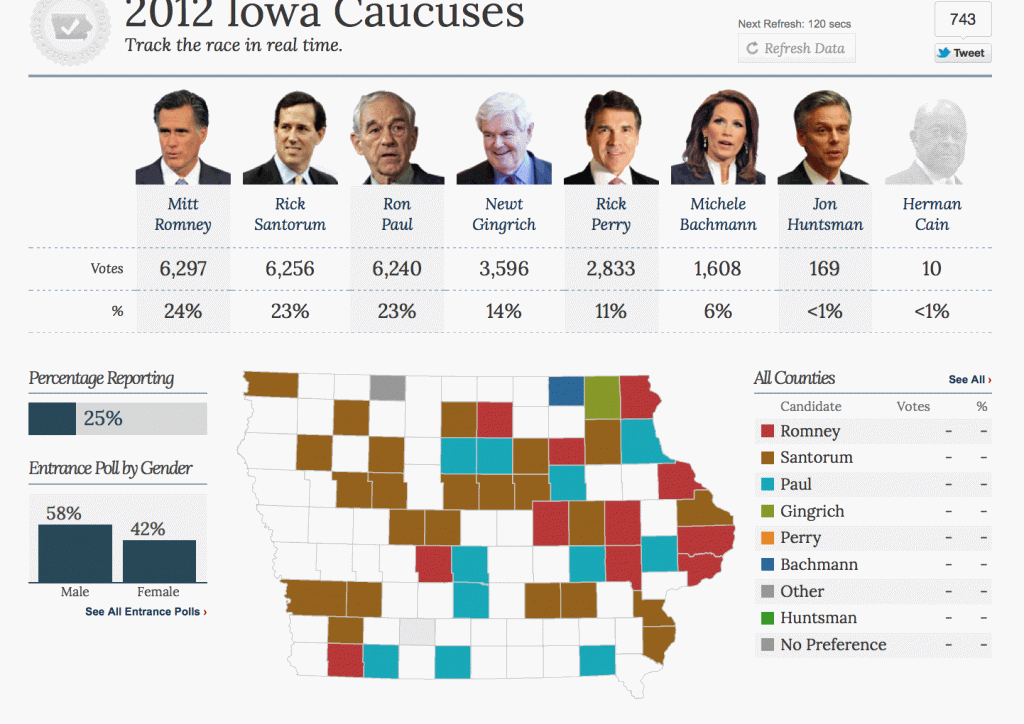
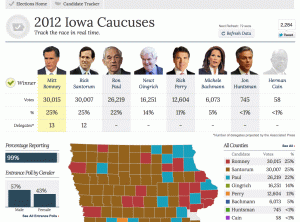
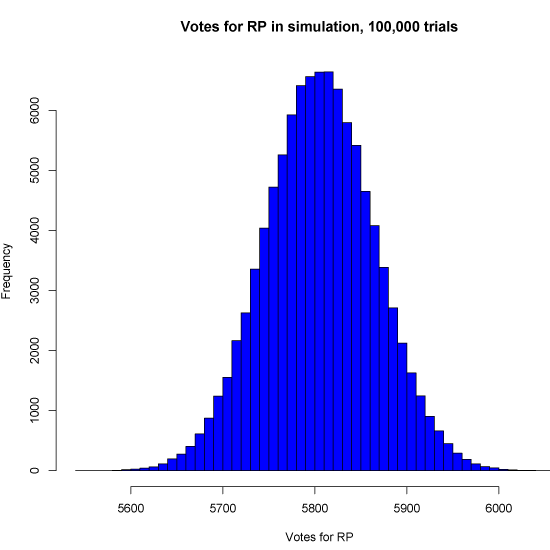
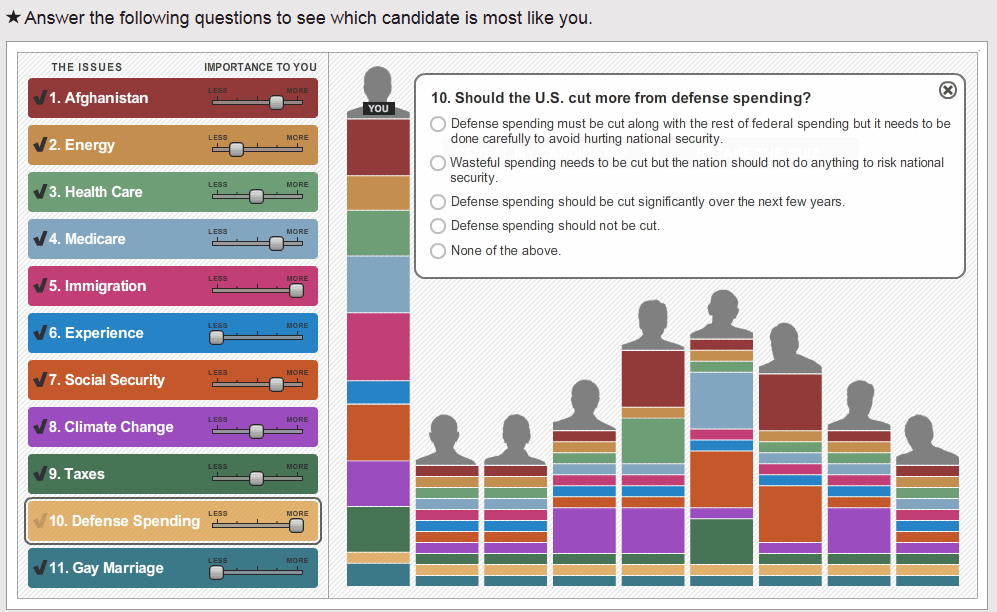
We often speak implicitly of different types of randomness but neglect to name or categorize them. Consider this post to be a kind of white paper or rough draft on the division of randomness into five categories. If you start using these distinctions explicitly, even if only in your own head, I think you will find them highly useful, as I have.
Type 0: Fixed numbers or known outcomes
Type 0 randomness is the special case of randomness where the data are already known. Any known outcome, regardless of the process that generated it, is Type 0 randomness. Once known, it has become a constant. In terms of information conveyed, all Type 0 randomness has zero informational entropy (a measure of uncertainty), and all messages with zero entropy are examples of Type 0 randomness.
Type 1: Pseudo random.
Most computers generate random numbers by a deterministic process. An initial “seed” is picked using some environmental factor, like the microsecond timing of the CPU, and from there onward every number that follows is fully determined by the algorithm. These algorithms can be very good, in terms of producing sequences of numbers that have desirable qualities. Yet, if you know that the sequence comes from some variation of, say, the Mersenne Twister, then a single number or short sub-sequence might be enough to predict all the subsequent numbers. Even if you can’t guess at the underlying mechanism, algorithms like the Mersenne Twister eventually loop: once you’ve seen the whole sequence, all future numbers will be known exactly, and you will have Type 0 randomness.
Computer software isn’t the only source of Type 1 randomness. Card shuffling machines, if sufficiently precise in their operation, map each unique ordering of playing cards to a single final ordering. Learn how the machine works, and you will know how each initial ordering is transformed.
The key to Type 1 randomness is that it is fully reducible to Type 0, in principle. The data source is known to be determinate, but the code is yet to be cracked. With enough time, attention, or technical sophistication, the sequence can be fully mapped.
Type 2: Non-fully reducible
Most real world randomness, and in general the most interesting sources of randomness, are of Type 2. Data streams of Type 2 randomness are conditionally random in the sense that we are able to reduce the uncertainty related to them, but only up to a certain point. Our model predicts the value of some response variable based on the other data, and this prediction can be quite good. But with Type 2 randomness there will always be some uncertainty left over, conditional on us making the best prediction we can.
A typical example of Type 2 randomness would be predicting whether certain individuals will develop heart disease within the next 10 years. Without knowing any specifics about the individuals, it’s very hard to make accurate predictions. Once we know some basic data, such as age, sex, and weight, we can make a better prediction. Even more fine-grained detail — history of smoking, diet, exercise patterns — allow us to make even better predictions. Each study or experiment we do, if of sufficient quality, improves the predictions we are able to make. Yet the randomness is non-fully reducible in the sense that, no matter how good our prior information or model, we will never be able to predict with 100% certainty whether a person will develop heart disease.
Regression curves are attempts to understand Type 2 randomness by separating signal (the model, or conditionally determinant, part) and noise. Often this noise part is modeled with some maximum entropy distribution, like the Gaussian. This is our way of recognizing that beyond some limit, we can no longer reduce the randomness. There will always be some Type 3 randomness left over.
Type 3: Martingale random
One way to think about Type 3 randomness is to imagine a fair bet. If the true probability of an event happening is 1/2, then 1 to 1 odds make it martingale random. There’s nothing you can do to improve your expected return to above zero; nor is there anything you can do to decrease your exception to below zero. In a series of independent fair bets, strategy is irrelevant to expectation. Importantly, this doesn’t prevent you from adjusting the probability distribution for payoffs, if you are able to vary wager amounts and stopping times. For example, you could try the martingale betting strategy, which offers a high probability of making small gains in exchange for a small chance of catastrophic loss.
Martingale randomness implies that there is no disconnect between the “advertised” distribution and the true (or revealed) distribution. The theoretical “fair coin” you meet in textbooks is martingale random. Of course you have to be very careful in how you interpret the results of a real coin toss in terms of informational content. Maybe it isn’t martingale random after all!
Type 3 randomness is not limited to situations in which you have two equally probable outcomes. Anytime you are unable to reduce randomness beyond a particular limit of predictability, what’s left over is martingale randomness. In fact, through a process of “whitening,” signals that generate non-uniform randomness can be converted into uniform randomness. The opposite can be accomplished as well (though I’ve never heard it called “blackening”).
Type 4: Real randomness.
This is the real thing: baked-in, irreducible randomness. For a data source to be Type 4 random, it must be martingale random and it must come from a sequence that is not only unknown, but a priori unknowable. If Type 4 randomness exists, then God plays dice; randomness is “baked in” to the universe.
I suspect that if Type 4 randomness really does exist, then it will be impossible to prove.
General thoughts on types and some examples
The most important thing to note about these categorizations is that the type of randomness depends on your perspective. The cards you hold in your hand are Type 0 randomness to you, but to the person sitting across the poker table from you, they are Type 2 randomness. Your opponent can use any number of tools to try and do better than pure chance at guessing your hand (how much you bet, the look in your eyes, and of course the cards they hold). The type of randomness you perceive is a function of what you know.
All degenerate random variables (i.e. the indicator function for the entire sample space, which is always 1) are Type 0 randomness.
Most of the games we play have some element of Type 2 randomness. Kids will play games with Type 1 randomness, like War, which is deterministic for any given card shuffling, and could in theory be mapped out. Type 1 randomness can still be surprising to you, but if there is any skill involved it would have to be Type 2 randomness: entropy reducible in theory.
The concept of Type 3 randomness is connected with two important statistical concepts: sufficiency and coherence. Once you know the sufficient statistics from a data source (and, vitally, assuming your model about the data is correct), threre’s nothing more you can do to improve your confidence intervals or ability to make predictions. For example, if you know that your data source has a Poisson distribution and the points are uncorrelated, then once you know the mean, there’s no other piece of information that can improve your ability to predict new values from the distribution. Broadly speaking, martingale randomness satisfies the de Finetti conditions of coherence, in that odds assignments must match up with known probabilities, and internal consistency needs to be maintained.
If your dice are loaded, then you’ve got a generator of Type 2 randomness. Over time, you can make better and better predictions about how often the different numbers will come up. But you still won’t be able to predict, with certainty, the results of any given roll. If somehow you knew the exact probabilities for each face, then you could use these dice as a generator of Type 3 randomness.
In a sense, the very first number generated by your computer’s random number algorithm is martingale random. There’s no way, unless you know how the seed is generated from the CPU’s timing and can “see” the microseconds tick by, to predict the range in which that number will fall with greater accuracy than would be expected by chance alone. On the other hand, it could be argued that the decimal part of the CPU’s clock isn’t really uniformly distributed. There will be some slight bias towards lower numbers, which is natural for any distribution of numbers that “grows” in size, even if it cycles (see Benford’s Law, and note that it applies not just to the first digit of a number, but to secondary digits as well). With enough careful investigation, you might be able to convert that first seeded random number into a case of Type 2 randomness.
Type 3 randomness is the holy grail of randomization. Casinos want dice which are perfectly symmetric in weighting, and resistant to wear and tear that might cause bias. Assignments to treatment in a clinical trial should strive for martingale randomness. Failure to achieve martingale randomness, when it is required, can have highly negative consequences.
“Beating the house” at a casino involves turning Type 3 randomness into Type 2 randomness, with enough usable signal left to overcome the casino’s inherent advantage. Strategies like analyzing roulette spins to find bias, and most famously counting cards, have been successfully used. One group of geeks was able to turn the randomness of a Vegas lottery machine which followed a Type 1 sequence into Type 0. They made the tactical mistake of hitting two huge jackpots in a row, tipping off the casino that they had successfully cracked the code. From the casino’s perspective, you have an inverse classification problem: given how well players are doing, what can you infer about the type of randomness they are detecting? Those jackpot-winning geeks could have taken a lesson from code breakers in WWII, who thought carefully about how to use the information contained in the cracked messages without showing the Germans that their code had been broken and that the allies understood their messages as more than the white noise of Type 3 randomness.
Because what separates the Types is our knowledge, randomness can come from a generation process that is completely deterministic and known to others (Type 0). As far as I’ve been able to tell, the digits of pi (beyond the ones you have memorized) are martingale random. If I give you a sequence of digits, and tell you they come from somewhere after the trillionth digit of pi, and let you use any tools you want short of a computer, there’s nothing you could do in a single lifetime to predict additional digits with an accuracy greater than 1/10th. Note that while the tail digits of pi appear to be a source of martingale randomness, not all irrational (or even transcendental) numbers have unpredictable digits. As counterexamples, see Louisville’s or Chapperhorn’s numbers. Any data source of Type 2 or greater must be incompressible, in the sense that if the sequence has infinite length, no finite-length description of it can exist. If there were a finite-length algorithm that could re-create (or predict) the sequence, then it’s at most Type 1 randomness (until we figure out this algorithm, if need be by iterating over all possible algorithms, starting with the shortest, until we get there).
I’ve tried to make these categorizations as clear as possible, but there are still edge cases which are hard to place. As is always the case, the closer you look, the fuzzier things get. However, I think you will still find this categorization of randomness to be quite useful, especially as a tool to discuss edge cases. Consider for a moment Chaitin’s Omega, which is the probability (weighted by string length) that a given computer program, run in a fixed computing environment, halts. The first few digits of Omega, determined by very short programs which instantly halt or loop, are easy to figure out. But we know from Turing that the halting problem is, in general, undecidable. So at some point, the digits of Omega become unknown and unknowable. Nor can we know when they become unknowable! The digits of Omega make the transition from Type 0 randomness (known) to Type 1 randomness (we just need to run the programs and see if they halt or loop), to Type 2 randomness (we may be able to set upper and lower bounds for the next few digits, or make a likelihood prediction based on reasoning and past experience), to Type 3 randomness (only God could predict the 10,000th digit with better than chance accuracy) and perhaps, almost frighteningly, to Type 4 randomness (God’s in a back alley, shaking up the dice right now).