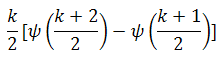r

feature / plot / r — 1 Comment
3
May 10

First annual R plot replication prize

Click image for the full-size version

$100 to the first person who can figure out how I created this plot and replicate it. Some hints:

  • It was done in R.
  • There is only one underlying probability distribution involved (one “rdist()“).
  • Including the “plot” statement, I created this with 3 short lines of code.

This is based on a random sampling of unstated size, so I don’t expect that your graph will be an absolute, exact match.

I’ll add $1 to the prize for every day that goes by without a winner until the end of the year. After that I’ll consider it an unsolved mystery and reveal the code I used.

Post your guesses for the code as a comment to this post. First correct answer wins. Good luck to all!

feature / r — 2 Comments
30
Apr 10

How many girls, how many boys?

I found this interesting question over here at mathoverflow.net. Here’s the question:

If you have a country where every family will continue to have children until they get a boy, then they will stop. What is the proportion of boys to girls in the country.

First off, there are some assumptions you need to make that aren’t stated in the problem. The most important one is that boys are just as likely as girls to be born. This is empirically false, but there’s nothing wrong with assuming it for the problem, so long as the assumption is acknowledged.

My first thought about solving the problem was to think about Martingales and stopping times, but that’s more complication than you need. If you look at it from the point of view of expectation things are simpler.The probability of having a boy first is 1/2, at which point the family stops and you have a ratio of 1 boy per 1 births. The probability of having one girl, then one boy is 1/4, at which point you have a ratio of 1 boy per 2 births. Multiplying the probabilities by the ratios and summing from 1 birth to infinity, you get an expectation of approximately 69.31% boys.

Problem is, this is the expectation for a single family. Because families who have more children (and thus more girls) contribute disproportionately to the pool of children, one family is a biased estimator for the proportion in the entire population. Douglas Zare at the above-linked mathoverflow question does a good job of working out the details for a country with an arbitrary number of families. Here is what he comes up with for the percentage of girls:

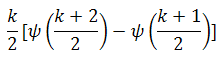
Where k is the number of families in the country, and 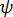 is the digamma function.

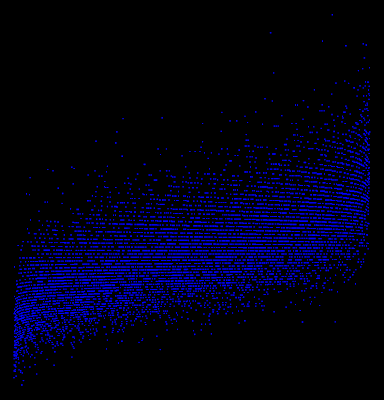
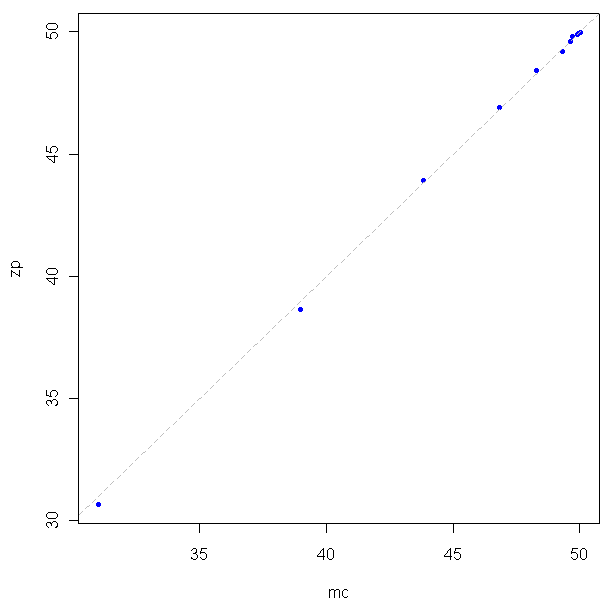
To be true to the new motto of this site, I decided to test this out in R using a Monte Carlo method. Here is my code:

And here is the resulting graph:

Looks like a good match.

Maybe you noticed that at the beginning I mentioned assumptions, as in more than one. We are also assuming that that all of the boys and girls, no matter how old, are still considered boys and girls. All of the parents were already in the country at the beginning of the problem, and then they all started having children until they had a boy and stopped. None of these children have had any children. The process is complete, and the new generation is the last. Obviously even if parents in a country did follow the rule of "babies until boy then stop", the results wouldn't match the theoretical because at any given moment there are many families in the process of still having kids. This is where, if I were so inclined or needed a more accurate model, I would dive back into the Martingale issue and things would get messy.

feature / plot / r — Comments Off on R: more plotting fun, this time with the Poisson
21
Apr 10

R: more plotting fun, this time with the Poisson

Click on image for a larger version. Here is the code:

par(bg="black")
par(mar=c(0,0,0,0)) plot(sort(rpois(10000,100))/rpois(10000,100),frame.plot=F,pch=20,col="blue")
feature / r — 2 Comments
11
Apr 10

R frustration of the day

Whenever you take a 1 column slice of a matrix, that gets automatically converted into a vector. But if you take a slice of several columns, it remains a matrix. The problem is you don’t always know in advance how big the slice will be, so if you do this:

You'll get an error if x is 1. This creates the worst kind of bug: an intermittent one that will hide until the right (wrong?) value of x occurs. To fix the problem you need to RE-declare the slice to be a matrix with ncol=x after you take the slice.

feature / plot / r — Comments Off on R: another nifty graph
8
Apr 10

R: another nifty graph

Make sure to click on the image to see the large version. Code for this graph:

moxbuller = function(n) {   
	u = runif(n)   
	v = runif(n)   
	x = cos(2*pi*u)*sqrt(-2*log(v))  
	y = sin(2*pi*v)*sqrt(-2*log(u))
	r = list(x=x, y=y)
	return(r) 
}
r = moxbuller(50000) 
par(bg="black") 
par(mar=c(0,0,0,0)) 
plot(r$x,r$y, pch=".", col="blue", cex=1.2)
feature / plot / r — Comments Off on R plotting fun
25
Mar 10

R plotting fun

Not easy to produce cool looking graphs in R, but it can be done. The results of some messing around are above. Here is the code I used:

x = runif(1000)
y = x/runif(1000)

cexes = 10*y/max(y) # For circle size
par(bg="black") # I see a white background and I want it painted black.
par(mar=c(0,0,0,0)) # Margins? We don't kneed no stinkin' margins.
plot(x,log(y), pch=20, col="white", cex=cexes)
feature / plot / r — Comments Off on R: Add vertical line to a plot
21
Mar 10

R: Add vertical line to a plot

If you have a plot open and want to add a vertical line to it:

abline(v=20) #Add vertical line at x=20
feature / r — Comments Off on R: Geometric mean
21
Mar 10

R: Geometric mean

gm(x)

But this requires package heR.Misc so you might as well just use:

exp(mean(log(x)))
feature / r — 3 Comments
20
Mar 10

R: remove all objects fromt he current workspace

feature / r — 3 Comments
20
Mar 10

R: Backwards for loop

 
for (i in 10:1) {
	print(i)
}

As easy as that.

← Older Entries
Newer Entries →