Summary/TL;DR
Either the first precincts to report were widely unrepresentative of Iowa as a whole, or something screwy happened.
Background
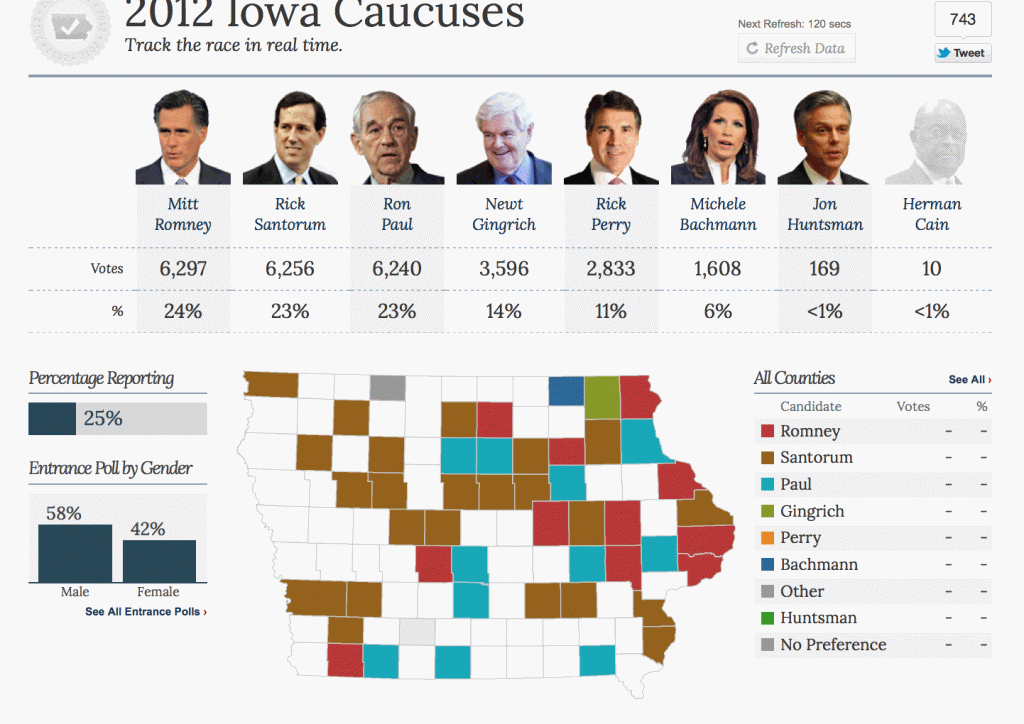
Yesterday was the first primary for the 2012 U.S. presidential elections. When I logged off the internet last night, the results in Iowa showed a dead heat between Ron Paul, Mitt Romney, and Rick Santorum. When I woke up this morning and checked the results from my phone, they were very different. So before connecting to the internet, I took a screen shot of what I saw before going to bed. Here it is:
Then I connected to the internet and refreshed that page:
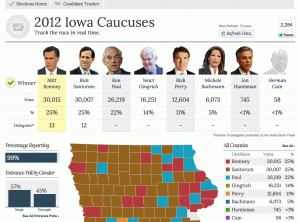
It seemed strange to me that the results should change so dramatically after 25% of the votes had already been recorded. As a statistician, my next question was: how unusual is this? That’s a question that can be tested. In particular, I can test how often you might have a split of voters like the one shown in the first screen shot, if the final split is like the one shown in the other screen shot, given that the first precincts to report were similar to later ones in voter composition.
That’s a lot to digest all at once, so I’m going to repeat and clarify exactly what I’m assuming, and what I’m going to test.
The assumptions
First, I assume the following:
1. That CNN was showing the correct partial results as they became available. Similarly, I am assuming that the amount shown with 99% of votes reported (second screen shot) is the true final tally, give or take some insignificant amount.
2. That the precincts to report their vote totals first were a random sampling of the precincts overall. Given how spread out these appear to be in the first screen shot, this seems like a good assumption. But that might not be the case. See the end of this post for more about that possibility.
3. No fraud, manipulation, or other shenanigans occurred in terms of counting up the votes and reporting them.
The test
Given these three assumptions, I’m going to come up with a numeric value for the following:
1. What is the probability that the split, at 25% of the vote tallied, would show Ron Paul, Mitt Romney, and Rick Santorum all above 6,200 votes.
It’s possible to come up with a theoretical value for this probability using a formal statistical test. If you decide to work this out, make sure to take into account the fact that your initial sample size (25%) is large compared to the total population. You’ll also need to factor in all of the candidates. Could get messy.
For my analysis, I used the tool I trust: Monte Carlo simulation. I created a simulated population of 121,972 votes, with 26,219 who favor Ron Paul, 30,015 who favor Mitt Romney, and so on. Then I sampled 27,009 from them (the total votes tallied as of the first screen shot). Then I looked at the simulated split as of that moment, and saw if the three top candidates at the end are all above 6,200 votes. What about just Ron Paul?
I’ve coded my simulation using the programming language R, you can see my code at the end of this post.
The results
Out of 100,000 simulations, this result came up not even once! In all those trials, Ron Paul never broke 6,067 votes at the time of the split.
I ran this test a couple times, and each time the result was the same.
Conclusion
If my three assumptions are correct, the probability of observing partial results like we saw is extremely small. It’s much more likely that one of the assumptions is wrong. It could be that the early reports were wrong, though that seems unlikely. The other websites showed the same information or very similar, so it seems doubtful that an error occurred in passing along the information.
Was there something odd about the precincts that reported early? This is not something you could tell just by looking at split vs final data. The data clearly show that the later precincts disfavored Ron Paul, but that’s just what we want to know: did they really disfavor him, or was the data manipulated in some way. The question is, were any of the results faked, tweaked, massaged, Diebold-ed?
To answer that question, we’d need to know if these later precincts to report were expected, beforehand, to disfavor Ron Paul relative to the others. It would also help to look at entrance polling from all of the precincts, and compare the ones that were part of the early reporting versus those that were part of the later reports. At this point, I have to ask for help from you, citizen of the internet. Is this something we can figure out?
UPDATE
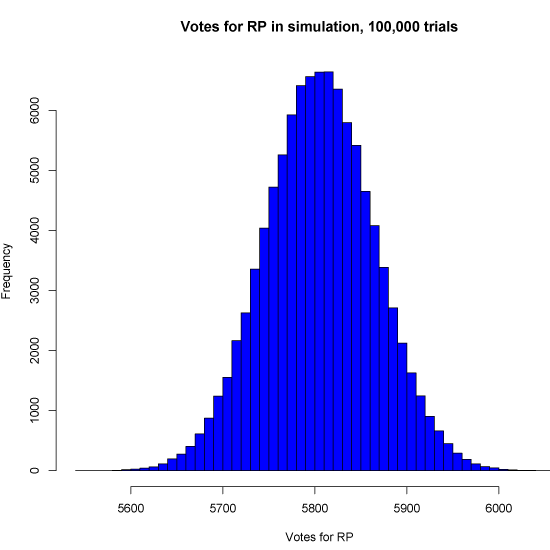
In case folks are interested, here’s a histogram of the 100,000 simulations. This shows the distribution of votes for Ron Paul as of the split, given the assumptions. As you can see it’s a nice bell curve, which it should be. Also note how far out on the curve 6,240 would be.
The code
Oh, one final possibility is that I messed up my code. You can check it below and see:
# Code for StatisticsBlog.com by Matt Asher
# Vote amounts
splits = list()
splits["MR"] = 6297
splits["RS"] = 6256
splits["RP"] = 6240
splits["NG"] = 3596
splits["JRP"] = 2833
splits["MB"] = 1608
splits["JH"] = 169
splits["HC"] = 10
finals = list()
finals["MR"] = 30015
finals["RS"] = 30007
finals["RP"] = 26219
finals["NG"] = 16251
finals["JRP"] = 12604
finals["MB"] = 6073
finals["JH"] = 745
finals["HC"] = 58
# Get an array with all voters:
population = c()
for (name in names(finals)) {
population = c(population, rep(name, finals[[name]]))
}
# This was the initial split
initialSplit = c()
for (name in names(splits)) {
initialSplit = c(initialSplit, rep(name, splits[[name]]))
}
# How many times to pull a sample
iters = 100000
# Sample size equal to the size at split
sampleSize = length(initialSplit)
successes = 0
justRPsuccesses = 0
# Track how many votes RP gets at the split
rpResults = rep(0, iters)
for(i in 1:iters) {
ourSample = sample(population, sampleSize, replace=F)
results = table(ourSample)
rpResults[i] = results[["RP"]];
if(results[["RP"]]>6200) {
justRPsuccesses = justRPsuccesses + 1
if(results[["MR"]]>6200 & results[["RS"]]>6200) {
successes = successes + 1
}
}
}
cat(paste("Had a total of", successes, "out of", iters, "trials, for a proportion of", successes/iters, "\n"))
cat(paste("RP had a total of", justRPsuccesses, "out of", iters, "trials, for a proportion of", justRPsuccesses/iters, "\n"))

The problem your simulation assumes equal distribution of support across precincts. According to the entrance polls 50% of his support came from voters under 40. Those voters are going to be clustered into relatively fewer precincts than other age cohorts. Since those precincts are going to be concentrated in more urban areas, it is much more likely to be reported earlier than more rural, older precincts where he did not perform well.
Are you suggesting older folks would be out later?
Remember the rule (GOP specific, AFAIK): you must be there at 7:00, must stay until 9:00 and vote. You may not be “late” and still vote.
what i found more weird was polk county..He was leading with 29 percent and look where he ended up.I agree though it seemed almost planned to get him down a couple of percentage points.i think he would have won by a percent if the fix was not in..But as Stalin said does not matter who votes but who counts them.This could only get worse in the closed primaris especially with electronic voting machines
What, you don’t believe in the perfection of Capitalism to run elections? They wouldn’t make machines easily adjusted to make Their Guy the Winner? Of course not.
We don’t have capitalism (free markets and free people). We have corporatism.
Mussolini coined a word for that. The Right Wingnuts get cranky when one mentions it.
Your approach is buggy. You forgot to account for the fact that results must be reported by precinct. The right experiment to carry out is to start with the actual reported distribution of votes in each precinct, and then carry out a simulation where you choose a random subset of the precincts as “early reporters” and total up their votes. With only tens of precincts this allows for far more statistical fluctuation than you get with hundreds of thousands of individual votes.
I agree it looks very unlikely that the first 25% of precincts reporting were a random sample of precincts, but your test seems not adequate to me.
The standard error of the estimated proportion of votes for a candidate from drawing 25% of 121,000 votes individually is incredibly small, at most on the order of 10^-3. So of course you’ll never see Paul’s numbers change so much if you assume an individual random draw.
I don’t know exactly how the Iowa voting and day of vote reporting works, but it looks from the map above there are something like 90 sub-divisions. That’s too big for individual caucuses, so presumably those are districts, and there are precincts within those districts. Still, say there are 1,000 precincts. Then you’re really getting a stratified sample from 1,000 strata. That still makes a 3% swing for Paul unlikely, but more in the realm of possibility if the order of reporting is truly random.
I appreciate the comments. Please note that the point of the simulation is to see *if* these results could happen randomly, without either 1. The early precincts being unrepresentative or 2. Something irregular occurring in the voting.
The simulation shows, with very high probability, that *either* 1 or 2 must be the case. If you have evidence or argument about either of those, post away.
I agree with your TLDR, it’s most likely un-representativeness of the early precincts. Unfortunately, CNN’s exit polls (and maybe others?) don’t have very large sample sizes. They also don’t indicate the geographical dispersion of the exit polling data.
Both of those things make it tough to back out any kind of information to analyze your #1. Interesting analysis, though, I liked it.
I’m also a data analyst developer/machine learning researcher. I was also totally floored by the difference between 25% and 99%.
The only other factor that you have maybe not mentioned is that you took the snapshot near its peek. Just like with the gtest, you can’t continuously take it and go with the first one that shows the challenger or champion with 99% significance because then there is selection bias (if you let the experiment go on longer it could have drifted down further).
That being said, from 24-24-24 Paul-Romney-Santorium at 25% to 21-24-24 at 99% is extremely unlikely given the assumptions you have laid out. Excellent blog post. I was thinking of writing the same thing, but I was too busy with work this morning.
It’s 1. The way the caucuses are conducted make voting fixing nearly impossible.
@Chris:
That’s not true. They have to plug these numbers into a computer or cell phone (read: small computer), which could easily be manipulated on the receiving end. In fact, it has been proven that this happened in ’92. The final vote-count was off by about 13% in Iowa that year. I believe the locals to be fair, but I do not trust the ones they give their numbers to.
Just to clarify, they were only watching one (1) district in ’92… they showed that it happened in that district, not throughout Iowa.
If it happened in the only county they were watching, it is safe to assume that it happened other places as well.
My first reaction was that “Gee, the final results are almost exactly the same as the initial ones, what is he talking about?”
You should be able to calculate this from first principles. How much statistics do you know? Also, where’s the chi-squared test? What’s the significance level for that? You would want to look at that before even bothering to do something more sophoisticated.
You are simulating partial reporting of all precincts; the correct model is full reporting of a subset of precincts, isn’t it? That, coupled with systematic effects that relate to when precincts report will almost certainly invalidate your simulation.
What if Ron Paul votes simply casted their votes earlier than voters for other candidates? As in, Paul voters get to the voting location earlier than other candidates.
I’m not entirely sure about the process, though. That would only work if they tallied the votes after every voter at each voting location was finished.
What if Paul voters went to locations where the voting was tallied more quickly? Smaller communities would take less time to count votes for, and I think that means the votes would be reflected earlier on.
I think the issue with this is the “early voters” and late voters” CNN was talking about. Many of these early voters (ones to arrive at the caucuses early) were for Paul. Paul supporters, like myself, are WAY more enthusiastic about him, than supporters of the other candidates. I think this fact would violate this study. Although 25% seems like a large enough sample, it is not random, because earlier votes=more enthusiastic=more Paul.
As I said above, my understanding of the GOP caucus isn’t akin to voting: walk in, cast ballot, walk out. The rule, again as it’s been explained to me: arrive no later than 7:00, take part in open-ended discussion, vote. Whether each precinct could decide when to end discussion and take vote, I don’t know. Whether every precinct enforced the no vote until discussion finished rule, I don’t know either.
Another possible skew factor: who runs the meetings? A: party regulars less likely to support Dr. Paul. These guys will have at least a bit of influence with some of the less fervent Ron Paul supporters.
I am so lost, but Ron Paul 2012 and thank you for taking the time to do this.
As others have commented, your modelling does not show any kind of “spurious” data, and in truth, does not require modelling, as there are analytical implications of the central limit theorem.
What you have shown is that there is a good chance that the votes that were counted were not random as a function of counting time.
What would make the counting process more predictable (from the initial tally), would be if votes were pooled, randomised, then re-distributed prior to counting. However, this could take just as long to move votes around, and there would be no change in the end counts.
More importantly, preferential voting would have altered the electoral outcome significantly.
1. Caucuses are not government elections, and do not use Diebold voting machines, which would be a misuse of government property. The parties would probably like us to forget the distinction.
2. The divisions on the map of Iowa are the 99 counties. We have far too many counties in Iowa, raising the cost of government, but keeping it close to the voters. With all the school consolidation and community businesses vanishing, we like to keep some things close. Precincts are far smaller than counties. 99 precincts would give 30,000 people per precinct. Iowa has 1784 precincts, so the voters among the 3,000,000 people in Iowa aren’t so crowded at 1680 people per precinct.
3. This is not an election. It is a caucus. (Just in case you didn’t read #1.) it is a group of party regulars deciding who to run from their precinct. The vote is manual.
4. Statistics is nice. Chaos theory says that it would be proof that the fix were in if the results were even across the whole range. Remember Dewey winning over Truman? Nope, neither do I.
5. This is not an election. It is a party event that is usually attended by party regulars only. It leaves out independent voters and third parties. It is not meaningful except that the two majority parties have the thing all sewed up, legally of course. (just in case you didn’t read #1 or #3.)
One point I wanted to make about a comment below about population dispersity, I was watching the maps via google and the Des Moines register throughout the night. I saw at 25% the counties that had been counted, what you couldn’t tell from the photo’s above was that more rural counties (ones without large cities on the live map) were turned in first, which agreeably would lean toward Santorum. I expected either Paul or Romney or both to skyrocket in vote totals from there, but oddly, in my opinion, it was Romney and Santorum.
The other oddity, was very early results were Paul/Romney 25, Santorum 23 and for the final votes to place Romney and Santorum within 7 votes of eachother, comeon….
This is a neat example- a great starting point for teaching Monte Carlo simulations!
I coincidentally happen to live in a rural county that reported early, and went in heavily for Paul (even once all precincts were in). As others have observed, it’s pretty easy to imagine that the early precincts weren’t completely representative, and here’s a factor that might have played a role: age. (Specifically, college students)
As commenters have pointed out, small precincts are likely to ring in first, since they had fewer votes to count. However, if you look at the “before” map, the rural extremities of the state didn’t really systematically have precincts reporting first. In fact, the Paul support in the early map is coming from a mix of places: some precincts in more heavily populated areas, some in towns/small cities that might be more liberal (Waterloo, Grinnell), and some from corners of the state that were just a mix (e.g., the southeast, which county by county went for “Anyone but Romney”: Paul, Santorum, and even Perry took the lead her).
So this got me thinking: why did precincts in my rural Paul-loving county (Poweshiek) report earlier than precincts in other rural Santorum-loving (or even Perry-loving) counties? One hypothesis is that the caucus was more efficient here, due to the help of those famously organized college kids. Maybe Paul supporters turned out as volunteers to help with the registration process, setting things up so that the opening business would move smoothly, collecting ballots, etc., so that the precinct here was able to report earlier?
I’ve never been to a caucus in a rural part of the state, but my voting experience in other states, run by retirees via the league of women voters, tells me that things can get slow in the check-in line (laboriously turning all those big pages, trying to see the names upside-down), and I imagine that the mechanics of collecting and counting the votes could be slower, too. In big precincts, things are probably well organized to run as smoothly as they can with so many people, but I’m imagining the difference between a small precinct with ten 75-year old volunteers vs. one with six 75-year olds and four 20-year-olds.
We already know that Paul support is highest among younger voters, though I haven’t seen any nifty R-generated maps trying to interpret the patchwork voting results with demographic data in this way. Maybe it’s as simple as “precincts with higher Paul support also had more Paul-supporting volunteers, and they were younger and moved things through faster”?
Check out this blog post, titled “Suspicious Iowa”: http://www.lewrockwell.com/politicaltheatre/2012/01/suspicious-iowa/
Its a caucus not an election. As long as Paul’s votes were counted fairly that’s fine. What most likely happened is the establishment GOP didn’t want Paul to win. So those supporting Perry, Bachman, and Gingrich were asked to change to Romney and Santorum. It’s not illegal just how it works.
That would only make sense if Santorum were less wacky than Paul. He’s *more* wacky. Both relative to Romney (well, many people think so based on MA; they’re wrong, the legislature and public kept him in check).
The only piece of info I’m dying to see is which counties were first and last to report in 2008 in order to help verify one of his assumptions that the first 25% truly was a purely random sample by comparing those results to 2012 (which could be analyzed by watching 2008 ticker tapes), and also to see if the counties time of official reporting in 2008 were consistent with 2012 in order to see if any funny business may have been happening in the more western counties.
With that said, the results seem consistent with 2008 when you analyze county by county.
2008:
http://www.cnn.com/ELECTION/2008/primaries/results/county/#I…
2012:
http://www.nytimes.com/pages/politics/index.html
In fact, it’s quite easy to show that the precincts or counties reporting first are not a random sample of all precincts. If you sum up all the votes in the first screenshot, the total is a little over 27000. That’s only 22% of the total number of votes, 25 % of the final number in the second screenshot is 30493.
It means that the precincts tallied early are smaller/have less voters than the average Iowa precinct. Of course, it does make sense but it means that we should not expect them to be representative of the rest of the precincts or the state as a whole.
You assume the districts are i.i.d., which is false, invalidating everything that follows.
@Ryan:
The districts don’t have to be “i.i.d.” for the analysis to work, they just have to report results in a non-systematic way/order. As per some other comments, the smaller ones seem to have reported first, though it seems they weren’t much smaller.
One more note about IID (Independent and Identically Distributed random variables, for those who are wondering). The districts themselves can’t be IID, I’m not sure how such a concept would even make sense. If by the districts you mean the demographics, you still have to be careful with your terminology. Generally we consider that these demographics aren’t the random variable. They are fixed (but unknown) constants. The random variable is the sampling statistic. The distinction here may seem subtle but it’s very important and worth taking time to understand. Perhaps I’ll write more about this in a blog post.
Who owns Diebold?
jus’ askin’
the Nov elections willbe tallied by Diebold
Wikipedia: “When elections are marred by ballot-box stuffing (e.g., the Armenian presidential elections of 1996 and 1998), the affected polling stations will show abnormally high voter turnouts with results favoring a single candidate. By graphing the number of votes against turnout percentage (i.e., aggregating polling stations results within a given turnout range), the divergence from bell-curve distribution gives an indication of the extent of the fraud.[21][dead link] Stuffing votes in favor of a single candidate affects votes vs. turnout distributions for that candidate and other candidates differently; this difference could be used to quantitatively assess the amount of votes stuffed. Also, these distributions sometimes exhibit spikes at round-number turnout percentage values.[22][23] High numbers of invalid ballots, overvoting or undervoting are other potential indicators.”
You need the raw data to do the analysis.
hey Fraud Science and expert data miners. The raw data maybe completely available from http://www.watchthevote2012.com
It’s just interesting to see how the final results fit or does not fit the Bell curve of expectancy. Can multiple null hypotheses be assumed? and then run against appropriate Monte Carlo simulations for the likelihood for most probable scenarios of the final results.
The MLE (assuming the sample is representative) would be that the proportions stay the same as in your initial point, whether that’s the partial or the full count.
Its also probably worth noting, aside from the 22 vs 25% issue in the total reporting, that the % reported for each candidate totals to 102% if Cain and Huntsman are left out.
But interesting discussion all.
@Justin:
The percentages were rounded off in the screen shot, which is why they don’t add to 100.
@Fraud Science:
Access to the raw data would be *very* nice. In particular, I’d like to “view” the data as it was reported, along with a timestamp for each report.
If anyone has access to additional data please let me know where to find it. Thanks.
There are 1,774 precincts in 99 counties or approximately 18 precincts per county. The second assumption of the analysis stating that ‘the precincts to report their vote totals first were a random sampling of the precincts overall’. The sample size is 25% of general population. We may expect that every fourth precinct is randomly selected to the sample. According to the first graph, the data were reported from 50 counties. It means that 49 counties don’t have even one precincts included to the sample. Is it plausible that the sample is random? Let’s assume that all counties contain the same number of precincts (18). The probability that a county doesn’t delegate even one precinct to the sample under the second assumption is 0.75^18=0.00563771.The expected number of counties that don’t have any precinct in the sample is 0.00563771*99≈1! The 97.5% quantile of the binomial distribution with parameters prob=0.00563771 and size=99 is 2. Thus, there is the strong evidence that the second assumption of the analysis is violated.
I’m confused; wouldn’t the *first* thing to come to mind be a violation of assumption 2? This is so easy to test– are there any characteristics of individuals or districts that predict inclusion in that first screenshot, and that also predict voting behavior?
I’m confused why this wouldn’t have been the first thing you did (before the MCS)– especially given that it seems to have taken a total of about 35 seconds’ worth of effort for several commenters to find overwhelming evidence in favor of a failure of assumption 2. Maybe then the MCS could have accounted for those differences and asked, “how strongly would these characteristics have to predict voting behavior, in order for that to be the explanation?”
Here’s a blog post: On a recent trip to Africa, I saw a herd of small white horses with stripes. It’s possible they were zebra. Alternatively, it is possible there is a cabal of shady characters wandering the continent painting stripes on horses under cover of darkness. Before I found that interesting, I’d need a little more evidence that they weren’t zebra.